ホーム ＞ リレーショナル・データベースの世界

類は友を呼ぶ



　SQL でデータを操作して様々な抽出を行う際、基本となる操作の一つが、データを何らかの基準に従ってグループ分けすることです。SQL を使うときに限らず、私たちは、日常生活の中でも、データを整理したり調べたりするときに、よくこのグループ分けという作業をします。

　SQL が持つ句の中で、グループ分けの機能を担うのが、GROUP BY と PARTITION BY です。この二つはどちらも、テーブルを指定されたキーで分割する働きをします。違うのは、GROUP BY の場合、分割後に集約して一行にまとめる操作が入ることだけです。

　たとえば、次のような幾つかのチームの構成メンバーを表すテーブルを例に取りましょう。


Teams
member team age
大木 A 28
逸見 A 19
新藤 A 23
山田 B 40
久本 B 29
橋田 C 30
野々宮 D 28
鬼塚 D 28
加藤 D 24
新城 D 22


　このテーブルに対して、GROUP BY句とPARTITION BY句を使うと、チーム単位の情報を得るクエリが書けます。どちらの句を使うにせよ、もとのTeamsテーブルを次のような部分集合に切り分けてから、SUM 関数で集約したり、RANK 関数で順位付けしたりしています。 

SELECT member, team, age ,
       RANK() OVER(PARTITION BY team ORDER BY age DESC) rn,
       DENSE_RANK() OVER(PARTITION BY team ORDER BY age DESC) dense_rn,
       ROW_NUMBER() OVER(PARTITION BY team ORDER BY age DESC) row_num
  FROM Members
ORDER BY team, rn;

db_gb_pb_3.gif

　パーティション・カットのイメージを図示するなら、下のようになるでしょう。

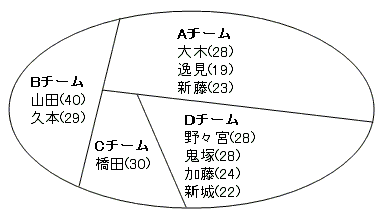
db_gb_pb_2.gif

　普通、集合は円で表すのが一般的ですが、ここでは、「分割（cut）」という操作のイメージを持ってもらうために、あえて直線で区切って部分集合を表現しています。

　さて、この作られた部分集合の性質に着目すると、次の三つの性質を持っていることが分かります。
  1. いずれも空集合ではない。
  2. 全ての部分集合の和が、分割する前の集合と一致する。
  3. 互いに異なる任意の二つの部分集合が共通部分を持たない。
　そもそもテーブルに存在する team 列の値で分割したのだから、分割後の集合が空集合になることはありえません[1]。また、分割後の部分集合を全部足しこめば、分割前の母集合が復元できることも自明です。言い換えれば、分割したことによって、行方不明になってしまうメンバーはいないよ、ということです。

　また、二つの部分集合に同時に属する（=同時に複数のチームに属する）コウモリみたいなメンバーも現れません。一人のメンバーは、必ず一つの集合に割り当てられます。つまり、GROUP BY や PARTITION BY は、各メンバーをチームに割り当てる関数なのだ、ということもできます。

　数学では、上の三つの性質を満たす部分集合の一つ一つを、「類(partition)」と呼びます。AチームからDチームまでの類をひとまとめにして「類別」と呼びます。主に群論などで使われる用語です。類という訳語は、分「類」という語感とも一致して、なかなか分かりやすいものです。

　もうお気づきでしょうが、種明かしをしてしまうと、SQL の PARTITION BY 句の名前は、この類の概念に由来しているのです。別に GROUP BY の方にこの名前を付けてもよかったと思いますが、GROUP BY の場合、カット後に必ず集約操作が入るので、多分、混乱を避けるために違う名前が使われたのでしょう。一般的に、一つの集合を類に分ける方法は複数あります。SQL でも、GROUP BY や PARTITION BY のキーを変えることで、作られるグループも変わりますよね。

　SQL で GROUP BY をけっこう頻繁に使うことからも分かるように、類は私たちの身の回りにたくさん存在します。たとえば、学校のクラスや出身都道府県などがそうです。生徒が一人もいないクラスは作る意味がありませんし、二つの県で生まれたという人もいないでしょう（出生地不詳の人はいるかもしれませんが、その人はNULLをキーとする類に入ります）。

　あるいは、トランプのカードなんかもそうです。52枚のカードは、マークの種類に従って4つに分類できますし、色なら2つに分類できます。同じ類に含まれた元同士は、共通の基準を満たしいているという意味で、いわば友のようなもの ―― 少なくとも違う類の元よりは近しい ―― と言えるかもしれません（数学ではこの友人関係を「同値関係」と表現します）。

　群論では、分類の仕方に応じて類に色々な名前が付けられていますが、そのうちの一つに「剰余類」というものがあります。これは、名前が表すとおり、整数を余りで分類した類です（一般的には類を数の集合に限る必要はないのですが、いまは単純に数だけを考えてください）。

　例えば、3で割った余りで自然数（N）を分類すると、

　余りが0の類：M1 = {0, 3, 6, 9, ・・・}
　余りが1の類：M2 = {1, 4, 7, 10, ・・・}
　余りが2の類：M3 = {2, 5, 8, 11, ・・・}

　というふうに分類できます。類の第2性質から、この3つの類は自然数全体を網羅します。数式で書けば、

M1 + M2 + M3 = N

です。これらを「3を法とする類」と呼びます。法は平たく言えば割る数のことで modulo の訳語ですが、こちらは、類と違ってちょっとイメージが湧きづらいですね。

　さて、すぐにピンと来た人もいるかもしれませんが、この法の概念も、やはり SQL に実装されています。そう、剰余の関数 MOD です。標準 SQL には入っていませんが、ほとんどの DB で使えます（% という演算子を使う実装もあります）。SQL で書くなら、さしづめこんな感じでしょうか。 

--1から10までを、3を法とする剰余類に分類
SELECT MOD(num, 3) AS modulo,
       num
  FROM Natural
ORDER BY modulo, num;

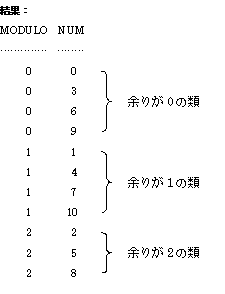
db_gb_pb_1.gif

　この剰余類というやつも、なかなか面白い性質を持っていて、色々な応用があります。一例を挙げると、剰余類は、もとの自然数の集合を等しいサイズの類に分割するので、大量データから特定の抽出率でサンプリングするときに便利なのです。たとえば、次のようなクエリを使えば、データ量を無作為に5分の1に減らせます（テーブルに連番列がない場合でも、ROW_NUMBER関数などで連番を振れば OK です）。 

--もとのテーブルから（ほぼ）5分の1の行数でﾅ抽出する
SELECT *
  FROM SomeTbl
 WHERE MOD(seq, 5) = 0;

--テーブルに連番列がない場合でも、ROW_NUMBBER関数を使えばOK
SELECT *
  FROM (SELECT col, 
        ROW_NUMBER() OVER(ORDER BY col) AS seq 
          FROM SomeTbl)
         WHERE MOD(seq, 5) = 0;

　もちろん、実際にはテーブルの行数がぴったり5の倍数になるとは限らないので、剰余類同士が完全に同じサイズにはなることはまれですが、「データを無作為に等分割する」というランダム・サンプリングの要件は十分に満たします。

　いかがでしょう、GROUP BY とPARTITION BY の動作のイメージ、および両者の理論的背景について、理解していただけたでしょうか。このように、SQL とリレーショナル・データベースには、集合論や、その発展版と言える群論などの成果が多く取り入れられています[2]。

　少し抽象的な話に感じたかもしれませんが ―― というかまあ、抽象的なんですが ―― まさに抽象的であることが、広い応用性を保証してもいるのです。数学の理論は、ただの現実離れしたお遊びではなく、日常の実務への豊富な応用を秘めています。でもそれはただ待っているだけでは見えてきません。自ら能動的に、実践と原理の間を架橋する努力をすることで、エンジニアとしての応用力も高まっていくのだと思います。


注
[1] NULL だけを含むという不気味な集合もありえますが、それは一応、空集合とは別物です。また、team 列に NULL が存在する場合は、これも薄気味悪い話ですが、NULL も類別のキーになります。
　なお、数学では、元の集合が空集合だった場合は、例外的に類も空集合一つだけ、ということに決められています。SQL の GROUP BY も、このケースでは正しく空集合を生成します。詳しくは、「空集合とNULL」の「SQLの欠陥 その１：空集合と集約関数」を参照。

[2] 例えば、群論の重要な概念の一つ、「冪等性」の応用については、「SQLで集合演算」を参照。

　

Copyright (C) ミック
作成日：2007/06/09
最終更新日：2017/06/22 b_entry.gif b_entry.gif
戻る