近年、リレーショナル・データベースと SQL に対する最もホットな批判の一つが、「リレーショナル・データベースでは木構造や階層構造のデータが扱えない/扱いにくい」というものです。特に最近は、Web 上でやりとりされるデータの形式に XML が普及してきたこともあり、データベースでも階層構造のデータを扱うことが切実な課題として浮上してきています。
このような問題に対して、データベース側からの解決策は二通りに分かれます。一つは、データベース・エンジンの機能を拡張する道です。実際、あんまり弱点弱点言われたからでしょう、この分野は最近、各ベンダの強化重点項目になっていて、Oracle の CONNECT BY 句をはじめ、各社とも多彩な独自拡張を試みています。この方向を突き詰めると、最終的には関係モデルそのものから脱却して、階層データの扱いに力点を置いた新たなデータ・モデルへ移行するところまで行きつきます。その代表格が XML データベースや多次元データベースです。NoSQLの一部もこうした方向に位置付けられるものがあります。
もう一つの道は、あくまで現行のリレーショナル・データベースの枠組みを与件とし、その範囲内で工夫することによって、何とかうまく木構造などを扱えるようにしようと模索する路線です。今回紹介するのは、この方向における興味深い成果の一つです。その実用性に関してはまだ賛否両論ありますが(特に後で見るようにパフォーマンス面での弱点が指摘されています)、SQL と RDB の豊かな応用可能性を示す独創的な方法論なので、DB エンジニアの方にはぜひ知っておいていただきたいと思います。
その方法の名前は、「入れ子集合モデル(Nested Sets Model)」と言います。従来のリレーショナル・データベースで階層データを扱うモデルには、「隣接リストモデル」や「経路列挙モデル」などが知られていますが、これらがデータ構造のイメージがつかみづらく、SQL も複雑で拡張性に乏しいという欠点を持っていたのに対し、直観的に理解しやすく、SQL も大変簡潔に書けるというメリットがあります。このモデルを提唱したのは、アメリカのデータベース界の重鎮の一人 J.セルコです。彼がこの方法論を考えついたのはもうずっと前のことですが、2004年、これを集大成した『Joe Celko's Trees and Hierarchies in SQL for Smarties』が出版されました。このサイトでは、同書の内容を中心に入れ子集合モデルによる木構造の扱い方を解説していきます。
1.入れ子集合モデルとは
木構造のデータ・サンプルとして、次のような階層の深さが 4 の組織図を例に取りましょう。一つのノードは、複数の親を持つことはない(=複数の上司を持たない)、かつ必ず一つの親を持つ(=命令系統から外れる社員がいない)と仮定します。この条件を破ると、木構造ではなくなってしまいます。
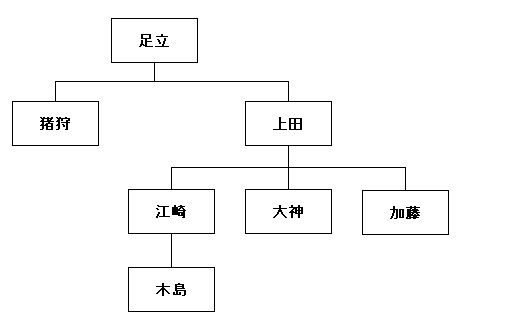
一般的な隣接リストモデルでこのデータを表現すると、次のようなテーブルになります。
--隣接リストモデルによる階層データ表現
CREATE TABLE OrgChart
(emp VARCHAR(32) PRIMARY KEY,
boss VARCHAR(32),
role VARCHAR(32) NOT NULL );
INSERT INTO OrgChart VALUES ('足立', NULL, '社長');
INSERT INTO OrgChart VALUES ('猪狩', '足立', '部長');
INSERT INTO OrgChart VALUES ('上田', '足立', '部長');
INSERT INTO OrgChart VALUES ('江崎', '上田', '課長');
INSERT INTO OrgChart VALUES ('大神', '上田', '課長');
INSERT INTO OrgChart VALUES ('加藤', '上田', '課長');
INSERT INTO OrgChart VALUES ('木島', '江崎', 'ヒラ');
emp boss role
---- ----- ----
足立 NULL 社長
猪狩 足立 部長
上田 足立 部長
江崎 上田 課長
大神 上田 課長
加藤 上田 課長
木島 江崎 ヒラ
一行が一人の社員(ノード)を表します。このモデルの鍵は boss 列にあります。この列が、自分が属する上司を表しています。当然のことながら、社長に上司はいませんので、社長だけはこの列が NULL になります。
このモデルは、SQL で木構造を表現する最もポピュラーな方法です。しかも驚いたことに、このモデルのアイデアの起源は、関係モデルの創始者 E.F.コッドまで遡ります。そのため、Oracle に代表される各ベンダが機能拡張に努める際も、基本的にこのモデルを使うことを前提にしています。なにしろ Oracle は、あの sott/tiger が持っている EMP 表がこの構造をしているのだから、最初からこのモデルを使うことを前提に製品を開発していたのではないか、という推測さえ成り立つぐらいです。
かくのごとく隣接リストモデルは、由緒正しいメジャーな方法ですが、実用的にはいくつかの問題を含んでいます。本稿の主旨ではないので詳細は省きますが、更新時に例外が発生したり、検索のクエリが(独自拡張を使わないと)自己結合の嵐になるなどの不便さがあります。そうした欠点に対処し、なおかつ標準 SQL のみを使用して階層データの取り扱いを実現する方法が、これから紹介する入れ子集合モデルです。このモデルは、隣接リストモデルとは対極的に、SQL の集合指向的な特性を十二分に利用したものです。
多くの優れたアイデアがそうであるように、基本的な発想はごく単純です。それは次の一言に要約されます。すなわち、
これだけ? そう、これだけです。後の話は全部、この基本命題の壮大な変奏に過ぎません。でもまあ、これだけじゃイメージつかめないでしょうから、ベン図とテーブル定義をお見せしましょう。
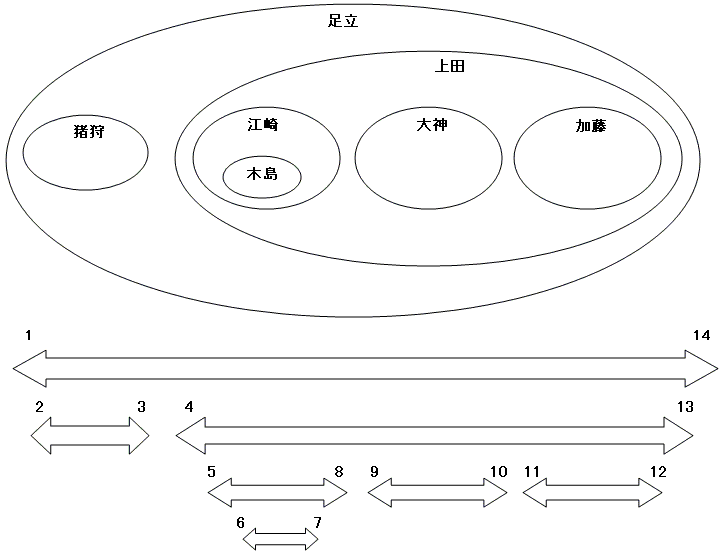
--入れ子集合モデルによる木構造の表現
CREATE TABLE OrgChart
(emp VARCHAR(32) PRIMARY KEY,
lft INTEGER NOT NULL,
rgt INTEGER NOT NULL,
CHECK (lft < rgt));
DELETE FROM OrgChart;
INSERT INTO OrgChart VALUES ('足立', 1, 14);
INSERT INTO OrgChart VALUES ('猪狩', 2, 3);
INSERT INTO OrgChart VALUES ('上田', 4, 13);
INSERT INTO OrgChart VALUES ('江崎', 5, 8);
INSERT INTO OrgChart VALUES ('木島', 6, 7);
INSERT INTO OrgChart VALUES ('大神', 9, 10);
INSERT INTO OrgChart VALUES ('加藤', 11, 12);
emp lft rgt
----------------
足立 1 14
猪狩 2 3
上田 4 13
江崎 5 8
木島 6 7
大神 9 10
加藤 11 12
一行が一人の社員を表すことは、隣接リストモデルと変わりません。違うのは、一次元の点として表現されていた木のノードを、直径と面積を持つ二次元の「円」、すなわち集合に見立てることです。lft と rgt は、円の左端と右端の座標を表します。従って、(rgt - lft)の値が楕円の水平方向の直径を表す、と言うことができます。このモデルに立って考えた場合、上司は、自分の腹の中に部下を抱え込むような格好になります。読んで字のごとく「腹心」です。集合の添え字は、左から右へ単調増加していくように割り振ります(初期データに添え字を割り振る具体的な方法は、3-7や3-8を参照)。また、あるノードの左端座標より右端座標のが大きいことは確実なので、それを CHECK 制約で保証しています。実際のところ、添え字は綺麗な連番である必要は特にないのですが、最初は分かりやすくするために歯抜けのない連番を振っておきます(頻繁に更新される木の場合、むしろ添え字にある程度の隙間を持たせたほうがパフォーマンス上のメリットがあるのですが、それはもっと後の話)。
これは、極めて大胆な視点の変換と言うべきですが、実は、セルコが自ら断り書きをしているように、木構造を入れ子集合によって表現するというアイデアそのものは、彼が思いついたわけではないのです。なんと、ドナルド・クヌースの古典的な教科書『The Art of Computer Programming』第1巻において、既にこの考え方が解説されています(邦訳の 304 ページ)。セルコは、このアイデアをデータベースにおいて応用したわけです。「私たちの世代の多くのプログラマがこの教科書で勉強したはずなのだが、今まで誰一人としてこの応用を思いつかなかったことは、まことに不思議である」と嫌味っぽいコメントまで述べています。あまりこういうことを口にする人ではないのですが、まあ自慢の一品であるという気持ちはよく分かります。これからさっそく見ていきますが、確かに、極めて独創的な ―― しかしある意味では正統的な ―― モデルなのです。
2.入れ子集合モデルを使った検索
さて、テーブルを作ったら、まずは検索から始めましょう。木のルートとリーフを探す簡単な方法から、ノード同士の階層関係を調べる方法など、いずれも階層データを扱うために必要不可欠の操作ばかりです。
2-1.ルートとリーフを探す
まず、基本となるの操作は、ルート(根)とリーフ(葉)を探すことです。ルートは親を持たないノードのことで、木構造には一つしか存在しえまえせん。この組織図で言えば社長の足立氏がそうです。一方、リーフはその反対で、子を持たないノードのことで、猪狩、木島、大神、加藤の四氏です。これらを求めることはとても簡単です。ルートは必ず左端の座標が 1 になる円なので、
--ルートを求める SELECT * FROM OrgChart WHERE lft = 1; emp lft rgt ---------------- 足立 1 12
一方、リーフは中に他の円を含まないため、必ず直径が1になります。
--リーフを求める SELECT * FROM OrgChart WHERE lft = (rgt -1); emp lft rgt ---------------- 猪狩 2 3 木島 6 7 大神 9 10 加藤 11 12
WHERE 句の条件は、素直に考えると「(rgt - lft) = 1」と書きたくなるかもしれませんが、上のような形のが良いでしょう。というのは、lft や rgt にインデックスを作成しておけば、左辺を裸単騎にすることでパフォーマンスが向上するからです。ちょっとした小技ですけど、このあたりもセルコはぬかりない。
実は、後で見るように、ノードの削除や追加をすると、リーフの直径が 1 より大きくなってしまう事態が生じます。そういう状況ではこのクエリは使えません。これに対処する一番良い方法は、添え字の欠番を埋めて、リーフの直径がちゃんと 1 になるよう調節することです(詳しくは3-5.添え字の欠番を埋める」を参照)。
しかし、リーフの直径が 1 でないケースに対応した汎用的なクエリもあります。リーフとは「下位の集合を一つも含まない集合」ということですから、NOT EXISTS を使えば朝飯前。
--リーフを求める(直径が 1 でなくても OK)
SELECT *
FROM OrgChart Boss
WHERE NOT EXISTS
(SELECT *
FROM OrgChart Workers
WHERE Workers.lft > Boss.lft
AND Workers.lft < Boss.rgt);
このサブクエリの条件に BETWEEN 述語を使うのは間違いなので注意してください。BETWEEN は両端を含むため、必ず自分自身を含んでしまうからです。あくまで不等号で書かねばなりません。ではついでに、この逆バージョンとして、lft が 1 でなくともルートを求めるクエリも紹介しておきましょう。
--ルートを求める(左端座標が 1 でなくても OK)
SELECT *
FROM OrgChart Workers
WHERE NOT EXISTS
(SELECT *
FROM OrgChart Boss
WHERE Workers.lft > Boss.lft
AND Workers.lft < Boss.rgt);
ルートとリーフは裏返し。従って「他のどの集合にも含まれていない集合」を求めればよいわけです。
2-2.ノードの深さを計算する
木の中で、あるノードの深さ、つまりレベルは、ルートとそのノードの間に存在するパス(経路)の数になります。パスは、図でいえばノード同士を結び付けている線に相当します。レベルの数値が大きくなればなるほど、そのノードはルートから遠くに位置することになります。入れ子集合モデルでは、パスを直接データとして保存しているわけではないので、深さも計算によって算出する必要があります。といっても、やることはごく単純な算数です。小学校で習った植木算って覚えてますか? 植木の本数とその間隔の数なんかを数える紛らわしい文章題で、答えが 1 だけずれることがよくあってむかっ腹を立てた記憶のある人も多いでしょう。いま、ノードを植木、パスを間隔とすれば、今回の問題は「両端に植木がある場合の植木算」です。
--ノードの深さを計算する SELECT Children.emp , COUNT(Parents.emp) AS level FROM OrgChart Parents, OrgChart Children WHERE Children.lft BETWEEN Parents.lft AND Parents.rgt GROUP BY Children.emp; emp level ------------ 足立 1 上田 2 猪狩 2 江崎 3 加藤 3 大神 3 木島 4
このクエリを平たく言えば、自分(Children.lft)の円を含む上司が何人いるかを数えているわけです。ただし、BETWEEN を使っているので、自分も数えています。もしレベルを 0 から始めたければ、不等号の条件に変えて自分を除外するか、あるいは単純に 「COUNT(Parents.emp) - 1」としてもいいでしょう。
この BETWEEN を使ってノード同士の包含関係を調べるクエリは、これから見ていく全てのクエリの基礎となります。従って、これをよーく理解しておいてください。
2-3.木の高さを計算する
これはさっきの問題の応用です。木の全体の高さを求めるには、さっき出したノードの深さの一覧の中から、最大値を選択すればよいわけです。先ほどのクエリをビューにすれば簡単ですね。
--木の高さを計算する
SELECT MAX(level) AS height
FROM (SELECT Children.emp , COUNT(Parents.emp) AS level
FROM OrgChart Parents, OrgChart Children
WHERE Children.lft BETWEEN Parents.lft AND Parents.rgt
GROUP BY Children.emp) TMP;
height
-------
4
Oracle は集約関数を入れ子にできるため、「MAX(COUNT(Parents.emp))」 という書き方もできます。ただしこれは標準 SQL 違反の独自拡張であるため、汎用性はありません。
2-4.木をインデント付きで表示する
入れ子集合モデルにおいては、一行が一つのノードを表しているので、ノードを列挙するのは簡単です。では、ノードの位置する階層を視覚的に表現するにはどうすればよいでしょう。一番お手ごろな方法は、結果の各行にインデントをつけてレベルを表してやることです。次のクエリを見てください。
--階層をインデントで表現する
SELECT LPAD(Mgrs.emp, LENGTH(Mgrs.emp) + CAST(COUNT(*) AS INTEGER) + 1, ' ') AS emp
FROM OrgChart Mgrs, OrgChart MidMgrs, OrgChart Workers
WHERE Mgrs.lft BETWEEN MidMgrs.lft AND MidMgrs.rgt
AND MidMgrs.lft BETWEEN Workers.lft AND Workers.rgt
GROUP BY Mgrs.emp, Mgrs.lft
ORDER BY MAX(Mgrs.lft);
emp
--------------
足立
猪狩
上田
江崎
木島
大神
加藤
これは、「2-2.ノードの深さを計算する」の応用です。ノードのレベルを COUNT(*) で計算し、その数だけ LPAD でスペースを先頭に追加しているわけです。ルートの足立氏が一番左に寄って、最も深いレベル(=ヒラのポジション)にいる木島氏が一人だけ右へ飛び出る形になります。
なお、LPAD 関数は実装依存の関数のため、Oracle、PostgreSQL、MySQL でのみ使用可能です。DB2 では REPEAT、SQLServer では REPLICATE 関数で、それぞれ代用することができます。
2-5.直属の親・子を取得する
隣接モデルの場合、直属の親を保持する列が存在するため、あるノードの従属関係を調べることは簡単でした。一方、入れ子集合モデルの場合、それほど直接的にはいきません。「直属」という関係は、「二つのノードの間に中間のノードが存在しない」という同値な条件に翻訳する必要があります。従って、テーブルを三つ使う自己結合が必要になります。
--親から見た場合の子供:その1
SELECT Parents.emp AS Boss, Children.emp AS worker
FROM OrgChart Parents LEFT OUTER JOIN OrgChart Children
ON Children.lft > Parents.lft AND Children.lft < Parents.rgt
WHERE NOT EXISTS
(SELECT *
FROM OrgChart MidParents
WHERE MidParents.lft BETWEEN Parents.lft AND Parents.rgt
AND Children.lft BETWEEN MidParents.lft AND MidParents.rgt
AND MidParents.emp NOT IN (Children.emp, Parents.emp));
boss worker
----- ------
足立 猪狩
足立 上田
猪狩
上田 江崎
上田 大神
上田 加藤
江崎 木島
大神
加藤
木島
子供のノードを持たない猪狩、大神などの人々の worker 列には NULL が現れます。しかしこれはちょっと複雑です。そこで、改良版として次のような SQL も考えられます。
--親から見た場合の子供:その2
SELECT Boss.emp AS boss, Worker.emp AS worker
FROM OrgChart Boss
LEFT OUTER JOIN OrgChart Worker
ON Boss.lft = (SELECT MAX(lft)
FROM OrgChart
WHERE Worker.lft > lft
AND Worker.lft < rgt);
これは、外部結合の結合条件で相関サブクエリを使い、自分を含む大きな円のうち、lft が一番大きい円が直属の上司である、という条件を記述しています。なかなか簡潔です。上司が何人の直属の部下を従えているかも、このクエリの結果を集約すれば簡単に求められます。
--親の持つ子供の数
SELECT Boss.emp AS boss, COUNT(Worker.emp) AS cnt
FROM OrgChart Boss
LEFT OUTER JOIN OrgChart Worker
ON Boss.lft = (SELECT MAX(lft)
FROM OrgChart
WHERE Worker.lft > lft
AND Worker.lft < rgt)
GROUP BY Boss.emp;
boss cnt
----- ----
足立 2
猪狩 0
上田 3
江崎 1
大神 0
加藤 0
木島 0
子供の数を数えるのに COUNT(*) ではなく COUNT(列名) を使っている点に注意してください。もし COUNT(*) を使った場合、結果は正しくなりません。なぜ正しくないか分からなかった方は、実際に COUNT(*) で実行してみた後に、「HAVING句の力」を参照してください。
反対に子供を主軸に見たい場合は、子供を主とした外部結合を使いましょう。
--子から見た場合の親
SELECT Boss.emp AS boss, Worker.emp AS worker
FROM OrgChart Worker
LEFT OUTER JOIN OrgChart Boss
ON Boss.lft < Worker.lft
AND Boss.lft = (SELECT MAX(lft)
FROM OrgChart
WHERE Worker.lft > lft
AND Worker.lft < rgt);
boss worker
----- ------
足立
足立 猪狩
足立 上田
上田 江崎
江崎 木島
上田 大神
上田 加藤
今度は、上司を持たないのはルートの足立氏だけなので、足立氏の行の boss 列だけが NULL になります。本当は、結合条件の「Boss.lft < Worker.lft」は論理的には不要なのですが(事実、PostgreSQL ではなくてもいい)、Oracle ではこれがないと正しく動作しないため、安全のため入れておきます。おそらく、外部結合のマスタとなるテーブルの列を結合条件に使わねばならない、という独自仕様の(困った)ルールがあるのでしょう。
このクエリは応用がきいて、入れ子集合モデルから隣接リストモデルへの変換もこのクエリを利用して行うことができます。詳しくは「3-8.入れ子集合モデルから隣接リストモデルへ変換する」を参照。
2-6.部分木を列挙する
木という構造は多くの興味深い特性があり、それゆえコンピュータ・サイエンスの分野でも非常に豊かな応用が見られます。そのような面白い特性の一つが、木の適当なノードを選択した場合、それをルートと見なすことで下位のノード群が再び木を構成することです。言い換えれば、木は再帰的構造である、ということです(だからこそ、入れ子集合という再帰的構造で表現できる)。このように大きな木の中に存在する木のことを部分木(subtree)と呼びます。今度は、子供を持つノードについて、それをルートとする部分木を列挙してみましょう。
--部分木を求める SELECT Mgrs.emp AS boss, Workers.emp AS worker FROM OrgChart Mgrs, OrgChart Workers WHERE Workers.lft > Mgrs.lft AND Workers.lft < Mgrs.rgt; boss worker -------------- 足立 猪狩 足立 上田 足立 江崎 足立 木島 足立 大神 足立 加藤 上田 江崎 上田 木島 上田 大神 上田 加藤 江崎 木島
もしある社員の左端座標がボスの円に含まれたなら、その社員はボスの配下に(直接または間接に)従属している、というわけです。このモデルにおいては、円同士が交わることはありえないため、右端座標についての比較は不要です(あっても構いませんが、冗長な条件なので結果は同じです)。もしルートに指定したいノードが決まっているなら、「Mgrs.emp = :root」のようにパラメータで渡してやれば良いでしょう。
2-7.パスを列挙する(列持ちバージョン)
ルートからあるノードまでのパスを、列持ちの形式で列挙してみましょう(行持ちの形式は次に見ます)。基本的には、自己外部結合を使った列展開でいけますが、このコードにはちょっと興味深いところがあります。まずはコードを見てもらいましょう。SQL にある程度慣れ親しんだ人なら「これは構文エラーではないのか?」と思うはずです。もしこのロジックを一目で納得できたら、あなたの SQL の実力は相当にハイレベルです(私はしばらくポカーンとしてしまった)。
--パスを列挙する(列持ちバージョン)
SELECT O1.emp,
(SELECT emp
FROM OrgChart
WHERE lft = MAX(O2.lft)) AS level_1,
(SELECT emp
FROM OrgChart
WHERE lft = MAX(O3.lft)) AS level_2,
(SELECT emp
FROM OrgChart
WHERE lft = MAX(O4.lft)) AS level_3
FROM OrgChart O1
LEFT OUTER JOIN OrgChart O2
ON O1.lft > O2.lft AND O1.rgt < O2.rgt
LEFT OUTER JOIN OrgChart O3
ON O2.lft > O3.lft AND O2.rgt < O3.rgt
LEFT OUTER JOIN OrgChart O4
ON O3.lft > O4.lft AND O3.rgt < O4.rgt
GROUP BY O1.emp;
emp level_1 level_2 level_3
---------------------------------
足立
猪狩 足立
上田 足立
江崎 上田 足立
大神 上田 足立
加藤 上田 足立
木島 江崎 上田 足立
ポイントは、スカラ・サブクエリ内の WHERE 条件で MAX 関数を使っていることです。一般的に、WHERE 句で MAX や SUM のような集約関数を使うことはできません。ところが、このコードは堂々とそれを使っています。しかも、これでれっきとした適法な構文です。反対に、ここで「lft = O2.lft」のように普通の列名を使うとエラーになります。なぜこんな常識と反対のことが起こるのでしょう?
その秘密は、最下行の GROUP BY 句にあります。GROUP BY 句で集約した場合、SELECT 句に書くことのできる要素は、
- GROUP BY句で指定した集約キー
- 集約関数
- 定数
ただし、ある意味で盲点を突いた技なので、動かない DB も少なからずあります。PostgreSQL では問題なく動作しますが、Oracle ではこの点がネックで動きません(おそらく構文解析において、「WHERE 句では集約関数は使えない」という教条的な判定をしているためでしょう)。こういう場合、「3-8.入れ子集合モデルから隣接リストモデルへ変換する」のクエリを一般化する方法が有効です。
--パスを列挙する(列持ちバージョン):そbフ2
SELECT O0.emp, O1.emp AS level_1, O2.emp AS level_2, O3.emp AS level_3
FROM OrgChart O0
LEFT OUTER JOIN OrgChart O1
ON O1.lft = (SELECT MAX(lft)
FROM OrgChart
WHERE O0.lft > lft AND O0.lft < rgt)
LEFT OUTER JOIN OrgChart O2
ON O2.lft = (SELECT MAX(lft)
FROM OrgChart
WHERE O1.lft > lft AND O1.lft < rgt)
LEFT OUTER JOIN OrgChart O3
ON O3.lft = (SELECT MAX(lft)
FROM OrgChart
WHERE O2.lft > lft AND O2.lft < rgt);
これならば、ほとんどの実装で動作するでしょう。このクエリは、SELECT 句のパスを結合して一つの文字列にすることで、経路列挙モデルへの変換にも利用できます。
2-8.二つのノード間のパスを探す(行持ちバージョン)
これは、2.6 の行持ち形式の部分木列挙に少し近いのですが、いま、最初から二つのノードが与えられていた場合、そのノードをつなぐパスを表示することを考えます。2.7 では列持ちで結果を表示しましたが、今度は行持ちにします。これは、次のように始点ノード(O1)と終点ノード(O2)に挟まれる中間ノード(O2)を求めることで可能です。path_order 列は、ノードをソートするときに使うと便利でしょう。
--ノード間のパスを検索する
SELECT O2.emp,
(O2.rgt - O2.lft) AS path_order
FROM OrgChart O1, OrgChart O2, OrgChart O3
WHERE O1.emp = :start_node
AND O3.emp = :end_node
AND O2.lft BETWEEN O1.lft AND O1.rgt
AND O3.lft BETWEEN O2.lft AND O2.rgt;
ただし、このクエリを使うときには一つ注意点があります。それは、一度レベルを上に上がらないと辿り着けないような検索ができないことです。例えば、加藤氏と木島氏をつなぐパスは「加藤 - 上田 - 江崎 - 木島」ですが、「加藤 → 上田」で上層に移動する必要があるため、うまくいきません。言い換えると、単調下降(というか単調上昇というか)のケースでしか動きません。
--単調下降の場合はOK
SELECT O2.emp,
(O2.rgt - O2.lft) AS path_order
FROM OrgChart O1, OrgChart O2, OrgChart O3
WHERE O1.emp = '足立'
AND O3.emp = '木島'
AND O2.lft BETWEEN O1.lft AND O1.rgt
AND O3.lft BETWEEN O2.lft AND O2.rgt;
emp path_order
------------------
足立 13
上田 9
江崎 3
木島 1
--上下移動が必要な場合はダメ
SELECT O2.emp,
(O2.rgt - O2.lft) AS path_order
FROM OrgChart O1, OrgChart O2, OrgChart O3
WHERE O1.emp = '加藤'
AND O3.emp = '木島'
AND O2.lft BETWEEN O1.lft AND O1.rgt
AND O3.lft BETWEEN O2.lft AND O2.rgt;
(結果は空)
さて、それではこのクエリを、上下移動する必要がある場合にも使えるように拡張する方法はあるでしょうか? これは、是非みなさんも考えてみてください。ちょっと難問だと思います。
2-9.二つのノードの相対位置を表示する
今度は、ノード間の関係を少し大雑把に分類してみましょう。つまり、二つのノードが、互いに親子の関係にあれば、そのように表示し、先ほどのように一度上昇せねば辿り着けない場合は「無関係」と表示しましょう。これは、円の中に「含まれる/含まれない」のテストをすることで簡単にできます。
--ノード同士の相対位置を表示する
SELECT CASE WHEN :first_node = :second_node
THEN :first_node || ' = ' || :second_node
WHEN O1.lft BETWEEN O2.lft AND O2.rgt
THEN :first_node || ' は ' || :second_node || ' の部下'
WHEN O2.lft BETWEEN O1.lft AND O1.rgt
THEN :second_node || ' は ' || :first_node || ' の部下'
ELSE :first_node || ' は ' || :second_node || ' と無関係' END
FROM OrgChart O1, OrgChart O2
WHERE O1.emp = :first_node
AND O2.emp = :second_node;
例えば、木島氏は上田氏をルートとする部分木に属するので、木島氏は上田氏の部下です。一方、江崎氏と加藤氏は、同じ階層なので上下関係はありません。よって「無関係」です(この際、個人的な交友はあったとしても無視します)。
--上田氏と木島氏の関係
SELECT CASE WHEN '上田' = '木島'
THEN '上田' || ' = ' || '木島'
WHEN O1.lft BETWEEN O2.lft AND O2.rgt
THEN '上田' || ' は ' || '木島' || ' の部下'
WHEN O2.lft BETWEEN O1.lft AND O1.rgt
THEN '木島' || ' は ' || '上田' || ' の部下'
ELSE '上田' || ' は ' || '木島' || ' と無関係' END AS rel_nodes
FROM OrgChart O1, OrgChart O2
WHERE O1.emp = '上田'
AND O2.emp = '木島';
rel_nodes
---------------------
木島 は 上田 の部下
--江崎氏と加藤氏の関係
SELECT CASE WHEN '江崎' = '加藤'
THEN '江崎' || ' = ' || '加藤'
WHEN O1.lft BETWEEN O2.lft AND O2.rgt
THEN '江崎' || ' は ' || '加藤' || ' の部下'
WHEN O2.lft BETWEEN O1.lft AND O1.rgt
THEN '加藤' || ' は ' || '江崎' || ' の部下'
ELSE '江崎' || ' は ' || '加藤' || ' と無関係' END AS rel_nodes
FROM OrgChart O1, OrgChart O2
WHERE O1.emp = '江崎'
AND O2.emp = '加藤';
rel_nodes
---------------------
江崎 は 加藤 と無関係
2-10.添え字に欠番がないか調べる
木に対して削除や追加などの更新を繰り返していると、添え字に欠番が生じることがあります。そういう場合でも、上で紹介してきたクエリはほぼ問題なく動作します。入れ子集合モデルにおいて、重要なのは各集合の包含関係なので、それぞれの集合の大きさや座標の絶対位置は大した問題ではないからです。しかしそうは言っても、多少の問題も生じます。例えば、リーフノードの直径が 1 より大きくなると、これを2-1の簡単なクエリで見つけることはできなくなります。
そこで、定期的に集合の添え字に歯抜けがないかチェックしましょう。方法はとっても簡単です。まず、lft と rgt をあわせた和集合のビューを作ります。インライン・ビューにしてもかまいませんが、このビューは作っておくと後々便利です。
--左端座標と右端座標の和集合 CREATE VIEW LftRgt(seq) AS SELECT lft FROM OrgChart UNION ALL SELECT rgt FROM OrgChart;
lft と rgt に重複はありえないので、和は UNION ALL で作れます。そうすると、欠番の有無は次のクエリでチェックできます。
--添え字の欠番チェック
SELECT CASE WHEN COUNT(*) <> MAX(seq) - MIN(seq) + 1
THEN '歯抜けあり'
ELSE '連続' END AS gap
FROM LftRgt;
もし欠番があれば「歯抜けあり」、なければ「連続」という定数を返します。これは、添え字の最小値が 1 でない場合でも正しく動作します。ロジックの詳細については、「HAVING句の力」と「帰ってきたHAVING句」を参照してください。
また、LftRgt ビューを使えば、で木全体に添え字を振りなおすことができます。これは「3-6.添え字の欠番を埋める」で行います。
3.入れ子集合モデルを使った更新
この章では、木やノードの追加・削除、あるいは木の中で動かしたりといった、木の形そのものをダイナミックに動かす方法について見ていきます。
3-1.部分木の削除
木の中から、部分木をごっそり削除することを考えます。いまはサンプルに会社の組織図を使っているので、それに即して言えば、社員をクビにすることに相当します。しかも、その解雇対象の社員が部下を持っている場合は、哀れ彼らも連座して解雇されます。これは、次のように解雇対象の社員の lft と rgt の範囲内に含まれるノードをごっそり削除することで実現できます。
--部分木の削除
DELETE FROM OrgChart
WHERE lft BETWEEN (SELECT lft FROM OrgChart WHERE emp = :fired_emp)
AND (SELECT rgt FROM OrgChart WHERE emp = :fired_emp);
例えば、江崎氏を解雇すると、連座して部下の木島氏も解雇されます。
--江崎氏を解雇(木島氏も連座)
DELETE FROM OrgChart
WHERE lft BETWEEN (SELECT lft FROM OrgChart WHERE emp = '江崎')
AND (SELECT rgt FROM OrgChart WHERE emp = '江崎');
--解雇後の組織図
emp lft rgt
------- ----- ------
足立 1 14
猪狩 2 3
上田 4 13
大神 9 10
加藤 11 12
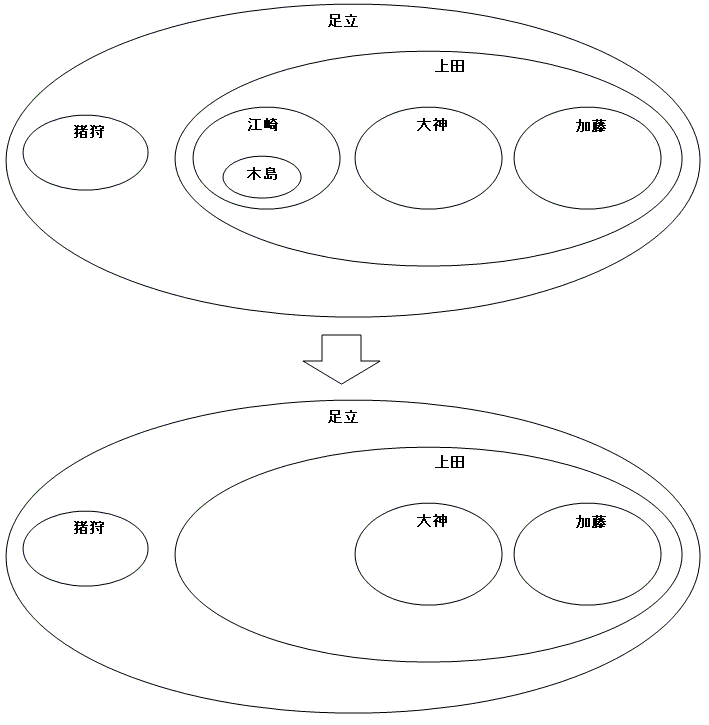
これだけだと、添え字の 5 ~ 8 が欠番になっています。そのままでもあまり実害はありませんが、念のため埋めておきましょう。プロシージャなどに組み込んで、事前に削除するノードの 左端座標と右端座標を変数 :drop_lft と :drop_rgt に保存しておけば、次のような 削除対象のノードより右のノードを左にずらす UPDATE 文が使えます。
--削除されたノードより右のノードを左に寄bケる
UPDATE OrgChart
SET lft = CASE WHEN lft > :drop_lft
THEN lft - (:drop_rgt - :drop_lft + 1)
ELSE lft END,
rgt = CASE WHEN rgt > :drop_rgt
THEN rgt - (:drop_rgt - :drop_lft + 1)
ELSE rgt END
WHERE lft > :drop_lft
OR rgt > :drop_right;
--更新後の組織図
emp lft rgt
------- ----- ------
足立 1 10
猪狩 2 3
上田 4 9
大神 5 6
加藤 7 8
3-2.単一ノードの削除
削除したいノードが中に子供を持たないリーフであると分かっていれば、迷わずそのノードを一行 DELETE しましょう。そのままだと添え字に歯抜けが生じるので、3-1や3-5の方法を使って、ギャップを埋めるのが良いでしょう。--単一ノードの削除 DELETE FROM OrgChart WHERE emp = :drop_emp;
一方、子供を持つ親ノードを削除する場合は、その子供(や孫)を誰が引き取るかに応じて、処理が二通りに分かれます。まず第一のパターンは、祖父母が引き取るケースです。このケースは、さっきのリーフと同様、削除対象のノードを削除するだけでかまいません。例えば、上田氏を削除した場合、江崎氏や大神氏は足立氏の保護下に入ります。
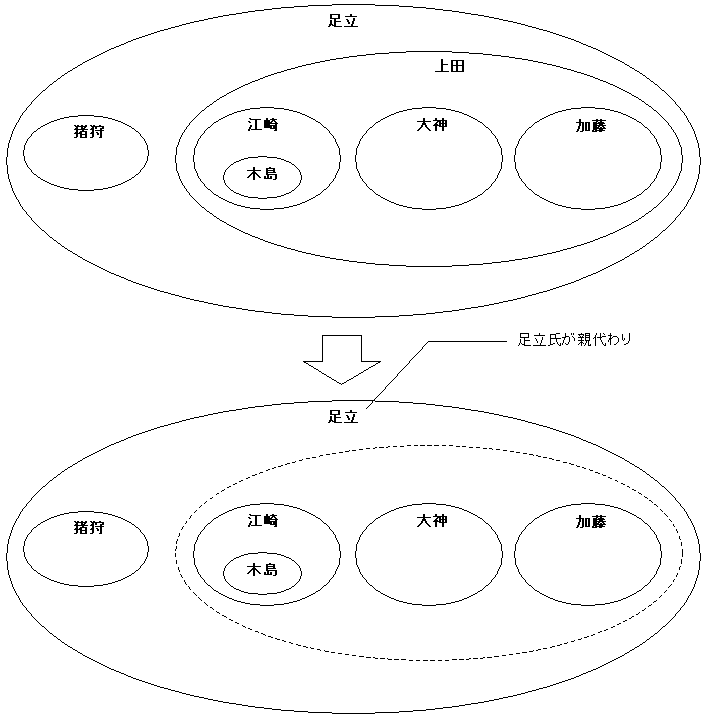
難しいのは、親の死後、子供の一人に家長の権限を委譲するケースです。この場合、複数の子供の誰を新たな「親」とするか、ルールを決める必要があります。今は最左端の江崎氏を後継者と見なして、上に立ってもらいましょう。イメージは次のようになります。
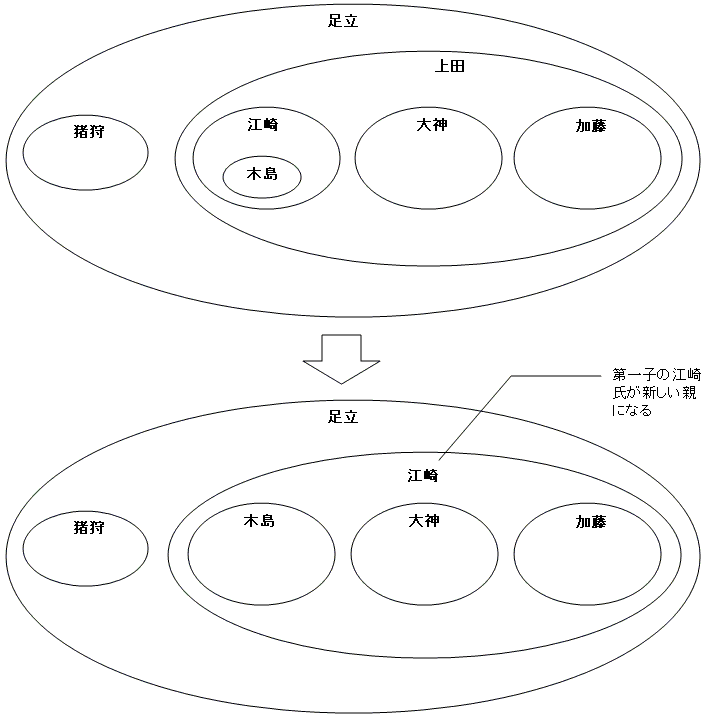
これを実現するには、二段階(見ようによっては三段階)を踏む必要があります。まず、削除対象のノードがリーフかどうかを判断して、リーフなら「削除対象」のマークを付けます。反対にもし子供を持っていれば、その子供の名前で更新し、子供に「削除対象」マークを付けます。そして第二段階で、マークを付けたノードを削除すれば無事世代交代は終了です。削除対象ノードの lft 値をパラメータ :drop_lft として入力します(場合に寄っては、これを求めることが第一段階になります)。
--第一段階:削除するノードにマーキング
UPDATE OrgChart
SET emp = CASE WHEN lft = :drop_lft --削除ノードがリーフの場合
AND lft + 1 = rgt
THEN '削除対象'
WHEN lft = :drop_lft
AND lft + 1 <> rgt --削除ノードがリーフでない場合
THEN (SELECT emp
FROM OrgChart
WHERE :drop_lft + 1 = lft)
WHEN lft = :drop_lft + 1 --削除ノードの第一子を削除対象とする
THEN '削除対象'
ELSE emp END;
--第二段階:マーキングしたノードを削除
DELETE FROM OrgChart
WHERE emp = '削除対象';
この方法は、さっきの単一ノードの削除までカバーできるすぐれものですが、実は DB によっては動かない可能性もあります。標準 SQL には沿っていますし、Oracle では正しく動作するのですが、問題となる点は以下の二つです。
- この更新が実行される最中、一時的に emp 列に重複が生じるため、主キー違反となる。
- UPDATE での更新時に同一テーブルの参照をサポートしていない。
--更新の途中、一時的に重複が発生する emp lft rgt ---------------- 足立 1 14 猪狩 2 3 江崎 4 13 ←「上田」を「江崎」に更新 江崎 5 8 木島 6 7 大神 9 10 加藤 11 12
しかし、更新の終了時点では、「江崎」が「削除対象」に塗り替えられるので、一意になりますし、制約の施行は文の終了時点で行われるものですから、この重複は、本来は問題のないものです。
一方、第二の理由によってエラーとなるのは、例えば MySQL です。これらの理由によって上の UPDATE 文が使えない場合は、もう少し手間のかかる方法を使わざるをえません。これは、皆さんの練習問題に残しておきましょう。
3-3.リーフを追加する
木にノードを追加するときは、リーフとして追加するのか、それとも親として追加するのかを決める必要があります。まずは、リーフの方から見ていきましょう。リーフを追加するには、どの親の配下に付けるかを決めねばなりません。その親より右にある既存のノードを右にずずずいっとずらし、空いた隙間に新しいノードを INSERT するわけです。そこで、新規ノードが追加される親の rgt をパラメータ :parent_rgt として渡してやります。
--第一段階:追加するノードの席を空ける
UPDATE OrgChart
SET lft = CASE WHEN lft > :parent_rgt
THEN lft + 2
ELSE lft END,
rgt = CASE WHEN rgt >= :parent_rgt
THEN rgt + 2
ELSE rgt END
WHERE rgt >= :parent_rgt;
--第二段階:ノードを追加する
INSERT INTO OrgChart VALUES ('国見', :parent_rgt, (:parent_rgt + 1));
例えば、猪狩氏の配下に新たに国見氏を加えるとすれば、次のようになります。
--第一段階:追加するノードの席を空ける
UPDATE OrgChart
SET lft = CASE WHEN lft > 3
THEN lft + 2
ELSE lft END,
rgt = CASE WHEN rgt >= 3
THEN rgt + 2
ELSE rgt END
WHERE rgt >= 3;
--猪狩氏より右のノードが右へずれ、隙間が瑞カまれる
emp lft rgt
---------------
足立 1 16
猪狩 2 5 --子供(3, 4)を持つ余裕が生まれた
上田 6 15
江崎 7 10
木島 8 9
大神 11 12
加藤 13 14
--第二段階:国見氏を追加する
INSERT INTO OrgChart VALUES ('国見', 3, (3 + 1));
この方法は、親が既に子供を持っていた場合は、新規追加のノードは末子、つまり一番右側に追加されることになります。もし既存の子供の間に割って入れたいなら、次の SQL を使います。
--第一段階:追加するノードの席を空ける
UPDATE OrgChart
SET lft = CASE WHEN lft > :child_rgt
THEN lft + 2
ELSE lft END,
rgt = CASE WHEN rgt > :child_rgt
THEN rgt + 2
ELSE rgt END
WHERE rgt > :child_rgt;
--第二段階:ノードを追加する
INSERT INTO OrgChart VALUES ('剣崎', (:child_rgt + 1), (:child_rgt + 2));
パラメータ :child_rgt は、追加するノードのすぐ左に位置するノードの右端座標です。この座標より右にある全ての座標を2ポイントずらせば、新しい子供を追加するスペースが生まれる、ということです。
3-4.親を追加する
既存のノードを含むような「親」として新たなノードを追加する場合も、考え方は基本的に同じです。違うのは、リーフの席を用意するときには、既存のノードを一律 2 ポイント右へずらせばよかったのに対し、今度は、追加するノードに含まれる子供たちは 1 ポイントだけずらし、追加ノードの右外に位置するノードを 2 ポイントずらす、という分岐が生じる点です。もちろん、この分岐は CASE 式で処理します。パラメータの :child_lft と :child_rgt は、追加するノードが含むべき子供の左端と右端です。ちなみに、複数の子供を抱えたい場合は、それらの子供のうち一番左の子供の lft と一番右の子供の rgt を使用します。
--第一段階:既存ノードの添え字をずらす
UPDATE OrgChart
SET lft = CASE WHEN lft BETWEEN :child_lft AND :child_rgt
THEN lft + 1
WHEN lft > :child_rgt
THEN lft + 2
ELSE lft END,
rgt = CASE WHEN rgt BETWEEN :child_lft AND :child_rgt
THEN rgt + 1
WHEN rgt > :child_rgt
THEN rgt + 2
ELSE rgt END
WHERE lft >= :child_lft
OR rgt >= :child_rgt;
--第二段階:親ノードを追加する
INSERT INTO OrgChart VALUES ('国見', :child_lft, (:child_rgt + 2));
例えば、大神氏と加藤氏の上司として国見氏を追加するなら、:child_lft = 9、:child_rgt = 12 を入力します。イメージとしては、下図のようになります。
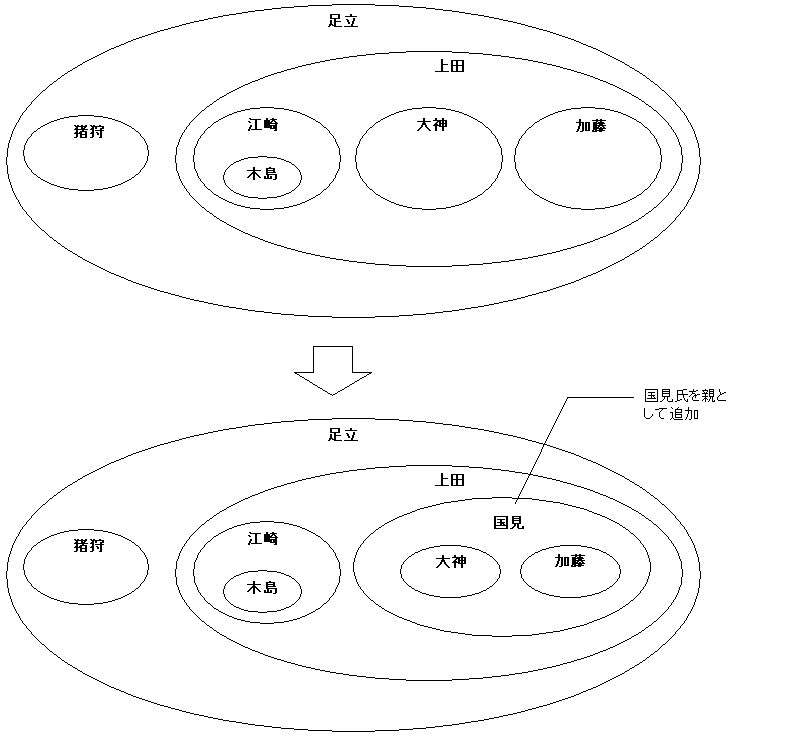
もちろん、現行のルートの上に覆いかぶせてやることも問題なく可能です。その場合は、ルートの左端と右端の座標を渡してやりましょう。
3-5.ノードを入れ替える
入れ子集合モデルでは、二つのノードをくるっと入れ替えることも簡単にできます。要するに、集合の添え字を入れ替えてやることと同義だからです。ではこの発展版として、部分木ごとごそっと入れ替える修正を考えましょう。これは、互いのノードに含まれるノードの添え字を全て変更対象とするため、少し大掛かりになります。いま、入れ替える二つのノードの添え字を (:lft_1, :rgt_1)、(:lft_2, :rgt_2) としましょう。最初のペアが左、後ろのペアが右に位置しているノードを表すとします。従って、:lft_1 < :rgt_1 < :lft_2 < :rgt_2 という関係が成り立ちます。すると、次のような UPDATE で可能です。
--部分木を入れ替える
UPDATE OrgChart
SET lft = CASE WHEN lft BETWEEN :lft_1 AND :rgt_1
THEN :rgt_2 + lft - :rgt_1
WHEN lft BETWEEN :lft_2 AND :rgt_2
THEN :lft_1 + lft - :lft_2
WHEN lft BETWEEN :rgt_1 + 1 AND :lft_2 - 1
THEN :lft_1 + :rgt_2 + lft - :rgt_1 - :lft_2
ELSE lft END,
rgt = CASE WHEN rgt BETWEEN :lft_1 AND :rgt_1
THEN :rgt_2 + rgt - :rgt_1
WHEN rgt BETWEEN :lft_2 AND :rgt_2
THEN :lft_1 + rgt - :lft_2
WHEN rgt BETWEEN :rgt_1 + 1 AND :lft_2 - 1
THEN :lft_1 + :rgt_2 + rgt - :rgt_1 - :lft_2
ELSE rgt END
WHERE lft BETWEEN :lft_1 AND :rgt_2
AND :lft_1 < :rgt_1
AND :rgt_1 < :lft_2
AND :lft_2 < :rgt_2;
例えば、猪狩氏と江崎氏を入れ替えるなら、(:lft_1, :rgt_1) = (2, 3)、(:lft_2, :rgt_2) = (5, 8) となります。
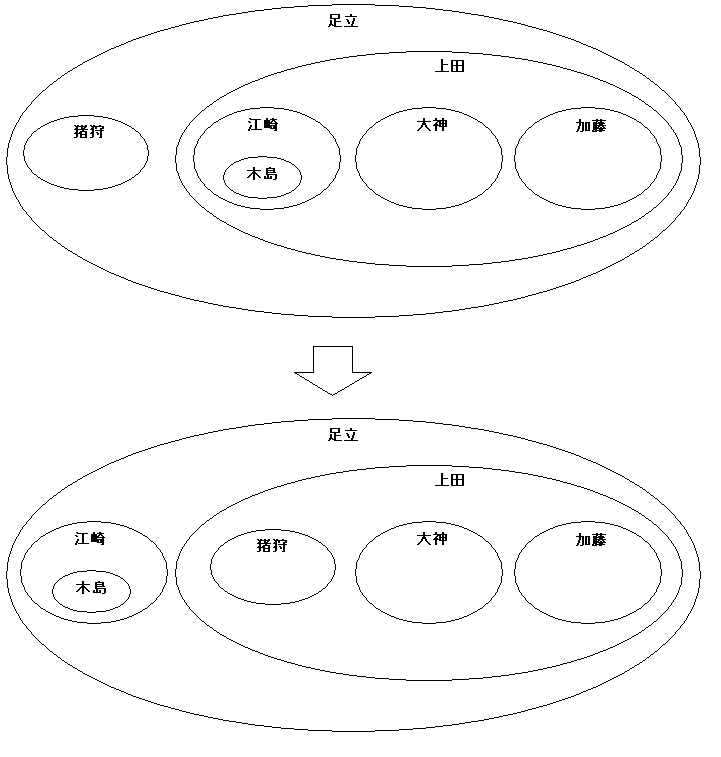
動作を簡単に説明すると、各添え字について、(1)左のノードに含まれているか、(2)右のノードに含まれているか、(3)左のノードと右のノードの真中に存在するか、(4)それ以外、という四パターンに分類して、添え字のずらし方を変えているのです。
なお、WHERE 句の最後の三つの条件は、パラメータが正しい大小関係にあるかどうかの妥当性をチェックするものです。もし渡されたパラメータが不正なら、条件が常に偽になるので一行も更新しません。いわば安全弁の役割を果たします。なかなか芸が細かいでしょう?
3-6.添え字の欠番を埋める
度重なる更新によって添え字にたくさんの歯抜けが生じた場合、これを綺麗に 1 から連番を振りなおしたいと思うことがあります。2-10で作った連番ビューを使えば、次の UPDATE 一発でOKです。
--木全体に lft と rgt を欠番なくふりなおbキ
UPDATE OrgChart
SET lft = (SELECT COUNT(*)
FROM LftRgt
WHERE seq <= lft),
rgt = (SELECT COUNT(*)
FROM LftRgt
WHERE seq <= rgt);
--こんな歯抜けだらけの汚い添え字も・・・
emp lft rgt
------- --------- --------
足立 7 1000
猪狩 20 30
上田 45 900
江崎 100 150
木島 111 120
大神 320 416
加藤 500 501
--更新後:綺麗すっきり連番に!
emp lft rgt
------- --------- --------
足立 1 14
猪狩 2 3
上田 4 13
江崎 5 8
木島 6 7
大神 9 10
加藤 11 12
更新前のテーブルの状態は、ルートの左端も 1 でなければ、リーフの直径もバラバラという散らかり具合でしたが、これがバシっと整理整頓されるのはなかなか爽快です。
全行を更新対象とするので、パフォーマンスが多少気がかりなところですが、lft と rgt にインデックスを張り、LftRgt ビューをテーブルとして実体化する(もちろん seq 列に主キーもつける)、というあたりまでやれば、かなり高速になるでしょう。
3-7.隣接リストモデルから入れ子集合モデルへ変換する
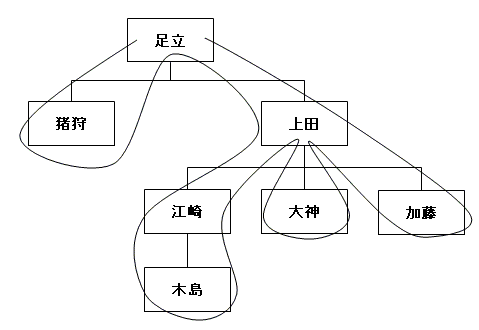
既に隣接リストモデルで作られたテーブルが存在する場合、これを入れ子集合モデルのテーブルへ変換したいという要望が当然出てくるでしょう。これを行う方法は、スタックを使った典型的な木の巡回アルゴリズムです。スタック、覚えてますか? LIFO 式のデータ構造です。驚かないで下さい、実は入れ子集合のテーブルは、スタック構造でもあったのです。手順としては、次のとおりです。まず、ルートから順に木をあますところなく走査して、見つけたノードをスタックに詰め込んでいきます(プッシュ)。その巡回のルートは、下図のようなイメージになります。セルコは「ノードを虫が辿っていくと想像せよ」と言っていますが、ちょうど曲線が虫の辿る経路だと思ってください。
この巡回アルゴリズムをコードにしたのが、次の解答です。SQL 単体ではなく、プロシージャを使用しています。ここでは、Oracleの PL/SQL のものを載せます。
--隣接リストモデルのテーブル
CREATE TABLE Tree
(node CHAR(10) PRIMARY KEY,
parent CHAR(10),
role CHAR(10));
INSERT INTO Tree VALUES ('足立', NULL, '社長');
INSERT INTO Tree VALUES ('猪狩', '足立', '部長');
INSERT INTO Tree VALUES ('上田', '足立', '部長');
INSERT INTO Tree VALUES ('江崎', '上田', '課長');
INSERT INTO Tree VALUES ('大神', '上田', '課長');
INSERT INTO Tree VALUES ('加藤', '上田', '課長');
INSERT INTO Tree VALUES ('木島', '江崎', 'ヒラ');
--入れ子集合モデルのテーブル
CREATE TABLE Stack
(stack_top INTEGER NOT NULL,
node CHAR(10) NOT NULL,
lft INTEGER,
rgt INTEGER);
--隣接リストモデルから入れ子集合モデルへ封マ換するプロシージャ
CREATE OR REPLACE PROCEDURE TreeTraversal
AS
counter INTEGER :=2;
max_counter INTEGER :=0;
current_top INTEGER :=1;
current_cnt INTEGER :=0;
BEGIN
--カウンタの最大値を初期化(一つのノードについて二度巡回するので2倍している)
SELECT COUNT(*) * 2 INTO max_counter FROM Tree;
--スタックの初期化
DELETE FROM Stack;
--ルートをプッシュ
INSERT INTO Stack
SELECT 1, node, 1, max_counter
FROM Tree
WHERE parent IS NULL;
--プッシュしたノードを元の木から削除
DELETE FROM Tree WHERE parent IS NULL;
WHILE counter <= max_counter- 1
LOOP
--プッシュしたノードが子を持つか調べる
SELECT COUNT(*) INTO current_cnt
FROM Stack S1, Tree T1
WHERE S1.node = T1.parent
AND S1.stack_top = current_top;
IF current_cnt > 0 THEN
-- ノードが子を持っていれば、子を一つプッシュする
INSERT INTO Stack
SELECT (current_top + 1), MIN(T1.node), counter, NULL
FROM Stack S1, Tree T1
WHERE S1.node = T1.parent
AND S1.stack_top = current_top;
-- プッシュしたノードを元の木から削除
DELETE FROM Tree
WHERE node = (SELECT node
FROM Stack
WHERE stack_top = current_top + 1);
-- カウンタとスタック・ポインタのインクリメント
counter := counter + 1;
current_top := current_top + 1;
ELSE
-- スタックをポップして、rgtの値を決める
UPDATE Stack
SET rgt = counter,
stack_top = -stack_top -- スタックのポップ
WHERE stack_top = current_top;
-- カウンタはインクリメントするが、スタック・ポインタはデクリメント
counter := counter + 1;
current_top := current_top - 1;
END IF;
END LOOP;
END;
--実行後の Stack テーブル
node lft rgt
------ ----- -----
足立 1 14
上田 2 11
加藤 3 4
大神 5 6
江崎 7 10
木島 8 9
猪狩 12 13
このアルゴリズムのポイントは、一つのノードをプッシュしたら、それでそのノードとは「ハイ、さよなら」できるのではないことです。実際、最初にプッシュするタイミングでは、lft 値は 変数 counter を使えるのですが、rgt 値は NULL のまま保留にせざるをえません(ルートは例外的に rgt 値も決まる)。そのため、ノードを入れたら、それにぶら下がる子供たちを全てプッシュした後にもう一度戻ってきて、rgt 値を入れてやる必要があります。いわば「円を開く」作業と「円を閉じる」作業の二回、スタックされたノードへのアクセスが発生する点がかなめです(この「一つのノードが二回現れる」という現象は、XML から入れ子集合への変換でも問題になります)。
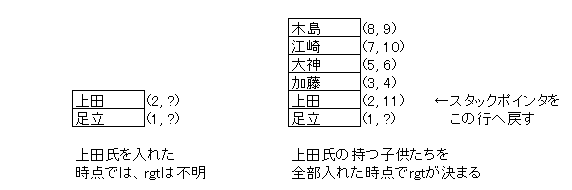
また、実行結果を見てお気づきの方もいるでしょうが、同じ階層に並ぶノードの順番が、微妙に食い違っています。例えば、猪狩氏と上田氏は、猪狩氏の方が若い順番に並ぶべきですが、この結果では逆転しています。これは、同じ階層内のノードから一つを選んでプッシュするときに、単純に「MIN(T1.node)」として文字コード上で前に来る名前の人物を選んでいるからです。本当は、きちんとした順序を示す列があるのなら、それを基準に若い順にプッシュするべきでしょう。
この方法においてもう一つ注意が必要なことは、このプロシージャを実行すると、元の隣接リストモデルのテーブルが空っぽになることです。そのため、実行する前は、念のためテーブルのバックアップを取っておくことを奨めます(まあ、次の節で見る逆変換を使えばまたテーブルを復元することも簡単ですが)。
どうでしょう。ちょっと驚いたんじゃないでしょうか。そうでもない?
3-8.入れ子集合モデルから隣接リストモデルへ変換する
入れ子集合モデルから隣接リストモデルの形式へ変換する方法は、非常に簡潔な方法が知られています。
INSERT INTO OrgChart_AL
SELECT Worker.emp, Boss.emp AS boss
FROM OrgChart Worker
LEFT OUTER JOIN OrgChart Boss
ON Boss.lft = (SELECT MAX(lft)
FROM OrgChart
WHERE Worker.lft > lft
AND Worker.lft < rgt);
emp boss
------------
足立
猪狩 足立
上田 足立
江崎 上田
大神 上田
加藤 上田
木島 江崎
これで見事、直属の上司の値を「boss」列に保持するポインタ・チェインの形式に変換できました。考え方としては、自分(Worker)を含むような大きな集合のうち、一番右の lft 値を持つ(すなわち最大の lft を持つ)円が自分の直属の上司(Boss)である、という条件を記述しています。
3-9.入れ子集合モデルから経路列挙モデルへ変換する
経路列挙モデルへの変換は、「2-7.パスを列挙する(列持ちバージョン)」のクエリを、ほとんどそのまま使えます。
--経路列挙モデルへの変換
INSERT INTO OrgChart_PE
SELECT O0.emp, COALESCE(O3.emp || '/', '') || COALESCE(O2.emp || '/', '') || COALESCE(O1.emp || '/', '') || O0.emp
FROM OrgChart O0
LEFT OUTER JOIN OrgChart O1
ON O1.lft = (SELECT MAX(lft)
FROM OrgChart
WHERE O0.lft > lft AND O0.lft < rgt)
LEFT OUTER JOIN OrgChart O2
ON O2.lft = (SELECT MAX(lft)
FROM OrgChart
WHERE O1.lft > lft AND O1.lft < rgt)
LEFT OUTER JOIN OrgChart O3
ON O3.lft = (SELECT MAX(lft)
FROM OrgChart
WHERE O2.lft > lft AND O2.lft < rgt);
emp path
------ ---------------------
足立 足立
猪狩 足立/猪狩
上田 足立/上田
江崎 足立/上田/江崎
大神 足立/上田/大神
加藤 足立/上田/加藤
木島 足立/上田/江崎/木島
COALESCE で途中のパスのノード列に NULL が返る場合に対処しています。
3-10.XML データを入れ子集合モデルに変換する
XML のようにタグで要素を記述するマークアップ言語では、開始タグと終了タグが存在するため、タグと要素が 1 対 1 ではなく 1 対 2 の関係になります。そのため、一つの要素を一行に変換するために工夫が必要になります。lft の値は開始タグが現れた段階で決められますが、rgt 値が簡単には分かりません。これを解決する方法が、「線形の入れ子集合モデル(The Linear Version of Nested Sets Model)」です。「線形」とは、データの流れを欠番なく単調増加する自然数で表現することからついた名前です。例えば、上で使ってきた組織図の XML データを例に取りましょう。
<社長 name="足立">
<部長 name="猪狩">
</部長>
<部長 name="上田">
<課長 name="江崎">
<ヒラ name="木島">
</ヒラ>
</課長>
<課長 name="大神">
</課長>
<課長 name="加藤">
</課長>
</部長>
</社長>
今の問題は、単純に行番号を添え字に使おうとすると、例えば、社長の足立氏は、一行目に出てくるので、lft 値は 1 とすぐ分かるのですが、rgt 値が最終行まで見ないと分からない、ということです。
この問題を解決するには、まず次のように XML の構造をそのままダイレクトに写し取ったテーブルを作ることです。
--OrgChart_XMLテーブル emp role seq ----------------- 足立 社長 1 猪狩 部長 2 猪狩 部長 3 上田 部長 4 江崎 課長 5 木島 ヒラ 6 木島 ヒラ 7 江崎 課長 8 大神 課長 9 大神 課長 10 加藤 課長 11 加藤 課長 12 上田 部長 13 足立 社長 14
見てのとおり、一人が二回現れるので、7人 × 2 の14行できます。seq 列の連番は、適当な方法で割り振ってください。データベースのシーケンス・オブジェクトを使っても良いですし、ホスト言語側で作成してもかまいません。単純に 「MAX(seq) + 1」を使ってもいいでしょう。その場合は、テーブルが空の場合にも対応できるよう「COALESCE(MAX(seq), 0) + 1」とするとなおよしです。
このテーブルができたら、あとは話は簡単。次のクエリで入れ子集合モデルのテーブルへ変換できます。
CREATE VIEW OrgChart_NS (emp, role, lft, rgt)
AS SELECT emp, role, MIN(seq), MAX(seq)
FROM OrgChart_XML
GROUP BY emp, role;
emp role lft rgt
----------------------
足立 社長 1 14
猪狩 部長 2 3
上田 部長 4 13
江崎 課長 5 8
木島 ヒラ 6 7
大神 課長 9 10
加藤 課長 11 12
このクエリが何をしているか、説明は不要でしょう。一人の人物について、seq の最小が lft、最大が rgt に相当するのです。これで、タグによって表現されたデータもスムーズに入れ子集合へと変換できます。「終了タグが遅れてやってくる」という難所を切り抜ける卓抜な方法です。今はビューを使いましたが、もちろん普通のテーブルへ INSERT してもいいでしょう。
なお、元の XML データが頻繁に変更されるタイプのものである場合は、seq 列は OrgChart_XML テーブルへデータを登録する時点ではなく、後の SELECT 文の中で ROW_NUMBER やスカラ・サブクエリを使って求めると煩雑なデータ更新に煩わされることがなくてよいでしょう。ただしその分、SELECT 文のコストが増すので、どちらのタイミングで連番を振るか、よく比較考量して使ってください。
4.木の構造を比較する
これまでは、一つの木についてその内部構造を調べたり、操作したりしてきました。しかし例えば、テーブルの環境を移動したり、バックアップをとったりしたときに、二つの木が同型であるか、全く同じノードを含んでいるのか、ということを調べる必要が生じることもあります。そこでここでは、二つの木を比較することを考えましょう。この比較をするときに重要な役割を果たすのが、集合演算子が持つ冪等性という性質を利用したテーブルの同一性チェックの方法です(詳細は「SQLで集合演算」を参照)。
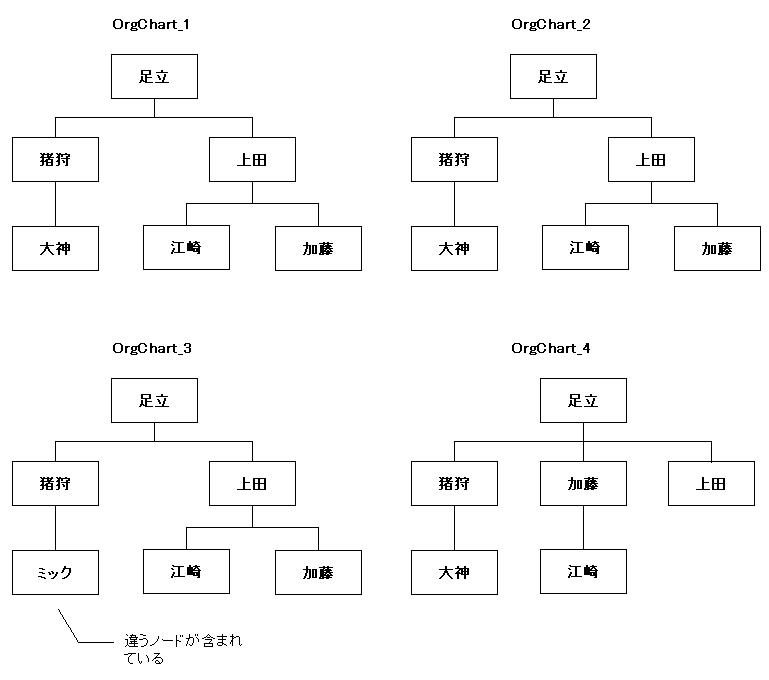
サンプル・データとして、次の四つのテーブルを用意しましょう。
CREATE TABLE OrgChart_1
(emp VARCHAR(32) PRIMARY KEY,
lft INTEGER NOT NULL,
rgt INTEGER NOT NULL,
CHECK (lft < rgt));
DELETE FROM OrgChart_1;
INSERT INTO OrgChart_1 VALUES ('足立', 1, 12);
INSERT INTO OrgChart_1 VALUES ('猪狩', 2, 5);
INSERT INTO OrgChart_1 VALUES ('大神', 3, 4);
INSERT INTO OrgChart_1 VALUES ('上田', 6, 11);
INSERT INTO OrgChart_1 VALUES ('江崎', 7, 8);
INSERT INTO OrgChart_1 VALUES ('加藤', 9, 10);
CREATE TABLE OrgChart_2
(emp VARCHAR(32) PRIMARY KEY,
lft INTEGER NOT NULL,
rgt INTEGER NOT NULL,
CHECK (lft < rgt));
DELETE FROM OrgChart_2;
INSERT INTO OrgChart_2 VALUES ('足立', 1, 12);
INSERT INTO OrgChart_2 VALUES ('猪狩', 2, 5);
INSERT INTO OrgChart_2 VALUES ('大神', 3, 4);
INSERT INTO OrgChart_2 VALUES ('上田', 6, 11);
INSERT INTO OrgChart_2 VALUES ('江崎', 7, 8);
INSERT INTO OrgChart_2 VALUES ('加藤', 9, 10);
CREATE TABLE OrgChart_3
(emp VARCHAR(32) PRIMARY KEY,
lft INTEGER NOT NULL,
rgt INTEGER NOT NULL,
CHECK (lft < rgt));
DELETE FROM OrgChart_3;
INSERT INTO OrgChart_3 VALUES ('足立', 1, 12);
INSERT INTO OrgChart_3 VALUES ('猪狩', 2, 5);
INSERT INTO OrgChart_3 VALUES ('ミック', 3, 4); --異なるノード
INSERT INTO OrgChart_3 VALUES ('上田', 6, 11);
INSERT INTO OrgChart_3 VALUES ('江崎', 7, 8);
INSERT INTO OrgChart_3 VALUES ('加藤', 9, 10);
--ノードは同じだが、構造が異なる
CREATE TABLE OrgChart_4
(emp VARCHAR(32) PRIMARY KEY,
lft INTEGER NOT NULL,
rgt INTEGER NOT NULL,
CHECK (lft < rgt));
DELETE FROM OrgChart_4;
INSERT INTO OrgChart_4 VALUES ('足立', 1, 12);
INSERT INTO OrgChart_4 VALUES ('猪狩', 2, 5);
INSERT INTO OrgChart_4 VALUES ('大神', 3, 4);
INSERT INTO OrgChart_4 VALUES ('加藤', 6, 9);
INSERT INTO OrgChart_4 VALUES ('江崎', 7, 8);
INSERT INTO OrgChart_4 VALUES ('上田', 10, 11);
OrgChart_1 と OrgChart_2 は、構造もノードも全く同じ、すなわちテーブル名が違うだけで集合としては完全に同一であると言うことができます。OrgChart_3 は、構造は 1, 2 と同じですが、木を構成しているノードが異なります。OrgChart_4 は反対に、ノードは全く同じですが、構造が異なります。
4-1.構造とノードが同一であるかの比較
構造も同型、使われているノードもピッタリ同じ、ということは、平たく言えばテーブルとして相等だということです。従って、単純にテーブルの相等性チェックのクエリが使えます。代表的なものは、次の二つです。
--木の相等性チェック:その1
SELECT CASE WHEN COUNT(*) = (SELECT COUNT(*) FROM OrgChart_1 )
AND COUNT(*) = (SELECT COUNT(*) FROM OrgChart_2 )
THEN '等しい'
ELSE '異なる' END AS result
FROM ( SELECT * FROM OrgChart_1
UNION
SELECT * FROM OrgChart_2 ) TMP;
--木の相等性チェック:その2
SELECT DISTINCT CASE WHEN COUNT(*) = 0
THEN '等しい'
ELSE '異なる' END AS result
FROM ((SELECT * FROM OrgChart_1
UNION
SELECT * FROM OrgChart_2)
EXCEPT
(SELECT * FROM OrgChart_1
INTERSECT
SELECT * FROM OrgChart_2)) TMP;
どちらのクエリも、1番と2番の木を比較したときのみ「等しい」を返し、残る組み合わせについては全て「異なる」を返します。パフォーマンスについては、どちらも似たりよったりだと思いますが、最初のクエリは UNION しか使わないので、INTERSECT や EXCEPT をサポートしていない MySQL や MS-Access でも使えるという利点があります。
4-2.ノードが同一であるかの比較
今度は、構造としての同型性は無視して、とにかく木に含まれているノードが同一なのかどうかを調べることを考えます。これもさっきのクエリを少し改変するだけで簡単に実現できます。要するに、今度は lft と rgt を無視して比較すればよいわけですから、この2列を除外しましょう。
--ノードの相等性チェック:その1
SELECT CASE WHEN COUNT(*) = (SELECT COUNT(*) FROM OrgChart_1 )
AND COUNT(*) = (SELECT COUNT(*) FROM OrgChart_3 )
THEN '等しい'
ELSE '異なる' END AS result
FROM ( SELECT emp FROM OrgChart_1
UNION
SELECT emp FROM OrgChart_3 ) TMP;
--ノードの相等性チェック:その2
SELECT DISTINCT CASE WHEN COUNT(*) = 0
THEN '等しい'
ELSE '異なる' END AS result
FROM ((SELECT emp FROM OrgChart_1
UNION
SELECT emp FROM OrgChart_3)
EXCEPT
(SELECT emp FROM OrgChart_1
INTERSECT
SELECT emp FROM OrgChart_3)) TMP;
今度は、1、2、4番の木は、互いにどれを比較しても「等しい」という判定になります。4番は構造は異なるものの、ノードは1、2番と同一だからです。一方、3番は他のどの木比較しても「異なる」とされます。「ミック」という邪魔者を含んでいるからです。もちろん、そもそも木の間でノードの数が不一致な場合でも正しく判定できます。
4-3.構造が同一であるかの比較
ではラストの問題です。今度は使われているノードは一切無視して、木の構造のみに着目します。とすれば、何を比較すればよいかは・・・もうお分かりですね。そう、(lft, rgt)の組み合わせが互いに完全一致するかどうかを調べればよいのです。入れ子集合モデルにおいては、木の構造は、ひとえにこの二つの座標のみによって表現されているのですから、残りの列はみなオマケみたいなものです。
--構造の同型性チェック:その1
SELECT CASE WHEN COUNT(*) = (SELECT COUNT(*) FROM OrgChart_1 )
AND COUNT(*) = (SELECT COUNT(*) FROM OrgChart_4 )
THEN '等しい'
ELSE '異なる' END AS result
FROM ( SELECT lft, rgt FROM OrgChart_1
UNION
SELECT lft, rgt FROM OrgChart_4 ) TMP;
--構造の同型性チェック:その2
SELECT DISTINCT CASE WHEN COUNT(*) = 0
THEN '等しい'
ELSE '異なる' END AS result
FROM ((SELECT lft, rgt FROM OrgChart_1
UNION
SELECT lft, rgt FROM OrgChart_4)
EXCEPT
(SELECT lft, rgt FROM OrgChart_1
INTERSECT
SELECT lft, rgt FROM OrgChart_4)) TMP;
木の構造としては、1~3の木は同型ですから、これらのどれを比較しても「等しい」となります。4番は、他のいずれとも異なる形をしているので、「異なる」と見なされます。同型性をチェックするときは、あらかじめ比較対象のテーブルを、3-6 の方法で欠番がないよう添え字を整理しておきましょう。でないと、同型なのに、添え字が汚いせいで不一致と判定されてしまいます。
5.経路列挙モデルについてのその他の情報
ここでは、他の言語、または様々なデータベースの実装で入れ子集合モデルを扱うためのライブラリやツール類、それに各種情報ソースを紹介しておきます。もし入れ子集合モデルが実用化されるならば、こうしたライブラリなどの充実は欠かせないでしょう。
5-1.他の言語で入れ子集合モデルを扱うためのライブラリ
MySQL と PHP で入れ子集合モデルを扱うためのライブラリについては、以下のサイトがフリーウェアとして提供しています。 PostgreSQL のニュースグループにも、このモデルを扱ったコードが掲載されています。 MS-Access のライブラリについては、以下を参照。5-2.入れ子集合モデルについての情報ソース
まずは必読文献から。セルコが10年以上にわたって研究してきた成果が集大成されています。入れ子集合モデルが主眼ではありますが、隣接リストモデルや経路列挙モデルについてもかなり詳細な解説があります。日本語で読める書籍としては、やはりセルコのこの本。第29章で入れ子集合モデルが解説されています(第28章が隣接リストモデル)。しかし、2001年刊行なので、やはりまだ情報不足で煮詰まっていない感がある。
同じく日本語の情報として、以下も参照。理論的解説よりも、隣接リストモデル、経路列挙モデル、入れ子集合モデルの三者についてのパフォーマンス比較がメインです。ちなみに、入れ子集モデルはけちょんけちょんにけなされています。
Web上で読めるものとしては、次のサイトが充実しています。タイトルに「MySQL」とついていますが、別に MySQL 以外のデータベースにも一般的に適用できます。参考にしている本が同じ『Joe Celko's Trees and Hierarchies in SQL for Smarties』なので、このサイトと内容がかなりかぶっています。
セルコの記事は Web 上でも読むことができます。
5-3.入れ子集合モデルが使われている実例
PHP のフレームワーク CakePHP は、ユーザのアクセスコントロールのための ACL テーブル群にこのモデルを採用しています。英文ですが以下のサイトの acos 、aros テーブルの構造についての解説が詳しい。
Web フレームワーク Ruby on Ralis は、ORM ライブラリの ActiveRecord の acts_as_nested_set メソッドにこのモデルを利用しています(しかしこの機能自体あまり利用されておらず、1.3 ではプラグインに格下げされると言われています)。
Copyright (C) ミック
作成日:2007/08/27
最終更新日:2017/06/22

 Tweet
Tweet