あらゆる命題は一つの内容と一つの形式を持つ。各語や記号の意味を抽象することで、つまり、命題の定項を変項で置き換えることで、純粋な形式の像が手に入る。(ただし語や記号が独立の意味を持っていることが条件である。)定項に適用される構文論の規則は、変項にもまた適用されなくてはならない。構文論という語の一般的な意味で私が意味するのは、どのような結合の場合にのみ語が意義(sense)を持つかを述べ[1]、それによって無意義な(nonsensical)構造を排除するような規則である。日常言語の構文論は、周知のように、この目的のためには適当でない。全ての場合において無意義な擬似命題(例えば「赤は緑より高い」や「実在はそれ自身において存在せねばならないが、また私自身にとってのものにもならねばならない」など)の構造を排除することができないからだ。
もし与えられた任意の命題を分析しようとするなら、私たちが一般的に気付くことは、諸命題はより単純な命題の論理和、論理積などの真理関数であるということだ[2]。しかし、分析が十分に行なわれたならば、もはやそれ自身はより単純な命題形式から構成されない命題形式に到達しなければならない。 [別の言い方をすれば] 私たちは最終的に、項同士の究極的結合へと到達せねばならない。その結合は、もし壊そうとすれば命題形式そのものを破壊せずにはおかない直接的結合である。私はそれを、B.ラッセルに倣って、原子命題(atomic proposition)と呼ぶ[3]。すると、この原子命題こそあらゆる命題の核であり、これらが原料を含むのであり、他の命題は全てこの原料の発展形にすぎない。私たちが命題の主題を探すべきは、原子命題に対してなのである。原子命題を発見し、それが語や記号からいかに構成されているかを理解することが、知識の理論の課題である。この課題は非常に難しく、哲学はまだ幾つかの点でこの問題に取り組み始めたばかりである。この問題に取り組むためには、どのような方法があるだろうか? 一つのアイデアは、日常言語 [の表現] では際限のない誤解を生み出すことを、適切な記号表現(symbolism)で表現するという方法である。つまり、日常言語が論理構造を隠す場合や擬似命題の形成を許す場合、一つの項が無数の異なる意味で用いられる場合、このような場合には、日常言語による表現を論理構造の明快な像を与えてくれる適切な記号表現で置き換え、 [それによって] 擬似命題を排除し、項を一義的に使用しなければならない。ところで、不正確な記号表現を明快な記号表現で置き換えることは、私たちが記述したいと思う現象を精査し、その論理的多義性を理解することによってのみ可能である。すなわち、正確な分析に到達することは、言ってみれば、現象それ自身に対する、ある意味でア・ポステリオリな論理的探究によってのみ可能であって、ア・プリオリな可能性について推測することによってではない。人はしばしば、ア・プリオリな観点から「結局のところ、原子命題の唯一の形式は何でありうるのか?」と問い、「それは例えば主語-述語命題であり、二項以上から成る関係命題であり、あるいは、述語や相互関係に関わる命題である」と答えたい誘惑に駆られる。しかし私の信じるところでは、これらは言葉の遊びに過ぎない。原子的形式を予見することはできない。そして、もし現実の現象がその構造だけしか私たちに伝えないとすれば、それは驚くべきことである。原子命題の構造について上述のように推測するよう導くのは、私たちの日常言語である。というのも、日常言語は主語-述語命題と関係命題を使っているからである。しかし原子命題を分析する場合には、日常言語はミスリーディングである。このことを比喩によって説明しよう。今、二つの平行な平面IとIIがあるとする。平面Iの上には、様々な大きさや形の楕円や長方形が描かれている。私たちがこれらの図形の射影を平面IIに作り出す方法は数多くあるが、そのうち次の二つの方法を考えよう。一つ目の方法は、正射影であれ何であれ、射影の方法を決め、平面Iの全ての図形をこの法則に従って平面IIに射影することである。二つ目の方法は、平面Iの楕円は全て円として、長方形は全て正方形として平面IIに射影されるという規則を立てることである。この方法は、何かの都合で平面II上に円と正方形だけを描きたい場合には便利である。ただしもちろん、平面IIの円と正方形から平面Iの元の図形を正確に直接推論することは不可能である。ただ、元は楕円か長方形だということが分かるのみである。元の図形の正確な形を知るためには、例えば、ある特定の楕円を私の前にある円に射影する個別的な方法を知らなくてはならないだろう。日常言語で [現実を射影する] 場合も、この場合と極めて類比的である。現実の事実が平面Iの楕円と長方形だとすれば、主語-述語形式および関係形式が平面IIの円と正方形に相当する。これらは私たち特有の言語の典型的な形式であり、実に多くの異なる論理形式が実に多くの異なる方法でこれらの形式に射影される。そしてまさにこの理由によって、記述された現象が実際に持っている論理形式について、これらのパターンの使用から結論を導くことは――極めて曖昧な結論を別にすれば――不可能なのだ。「この論文は退屈だ」とか「天気が良い」とか「私は怠け者だ」のような諸形式は、何一つ共有していないにも関わらず、主語-述語命題として、つまり、見かけ上は同じ形式の命題として現れる。
さて、私たちが現実の分析を理解しようとするとき、日常言語のパターンとはほとんど類似性を持たない論理形式を見出すことになる。空間と時間の形式によって、私たちは実に多様な空間的・時間的諸対象――色、音など――と対面する。それらの対象は、段階と連続的な推移を持ち、様々な比率で混ぜ合わされている。私たちの通常の表現手段では、その全てを把握することはできない。ここで私は、現実の現象に対する論理的分析について、第一の確定的な言明を述べようと思う。それは、現象を写像するためには、原子命題自身の構造に数(有理数および無理数)が含まれなくてはならない、ということである。これを私は次の例によって示したい。ある直交軸の体系、例えば、私たちの視野に描かれた交差する針金のようなものと、適当な物差を想像してほしい。すると明らかに、私たちの視野における色の斑点全ての形と位置を、座標系と選ばれる単位に関して意義(significance)のある数の言明によって記述することが可能である。また、この記述が適切な論理的多様性を持つこと、およびこの記述よりも少ない論理的多様性を持つ記述は、適切な論理的多様性を持たないことも、明らかである。
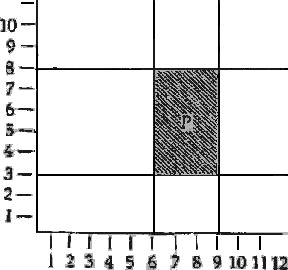
一つの単純な例は、「 [6-9, 3-8] 」という表現によって斑点 P を写像し、P についての命題、例えば「Pは赤い」を「 [6-9, 3-8] R 」という記号で写像することである。ここで「R」はまだ分析されていない項である。(また、「6-9」と「3-8」はそれぞれの数の間の連続的な区間を表現している。)この場合、座標軸は表現様式の一部であり、現実を私たちの記号表現に投影する投影法の一部である。一つの斑点が他の二つの斑点の間にあるという関係も、これと類比的に、見かけ上の変項を使うことで表現できる。言うまでもないが、この分析はいかなる意味でも完全ではない。私はこの分析において時間について何も言及していないし、単眼視の場合においてさえ、二次元空間を使用することは正当化されるものではない。私はただ、視覚現象の分析が行なわれるべきだと私が信じる方向と、この分析において、日常言語が私たちに期待させる論理形式とは全く異なる論理形式が見出せるということを指摘したいだけである。原子命題の形式に数が現れることは、私の意見では、特殊な記号表現だけの特性ではなく、写像の本質的な、従って不可避な特性なのである。そして数は――私たちが日常言語で話すならば――階層を認める性質、例えば区間の長さや音の高さ、色合いの明るさや赤さなどを扱うときに、これらのものの形式に含まれなければならない。一つの度合いが他の度合いを排除するというのが、これらの性質の特徴である。一つの色合いは、同時に二つの明るさや赤さの度合いを持つことができず、音もまた二つの強度を持つことができない。ここで重要な点は、これらの言明は経験を表現するものではなく、ある意味でトートロジーだということである。私たちの誰もが、日常生活においてはそのことを知っている。誰かから「外の気温は?」と訊ねられると私たちは、「華氏80度だ」と答える。その後もう一度彼から「90度かい?」と訊ねられたら、「80度だと、さっき言っただろう」と答えるだろう。 [この例も示すように] 私たちは度合い(例えば温度)についての言明を、補完を必要としない完全な記述とみなしている。従って時間を訊ねられれば、何時であるかを答えるが、何時でないかまでは答えないのである。
人はこう考えるかもしれない――かく言う私も少し前までそう考えていたのだが――性質の度合いを表現する言明は、量についての単一の言明とこの言明を完成させる補完的言明の論理積に分析できる、と。ちょうど、ポケットの中身を「1ペニーと1シリングと二つの鍵、他には何もない」と記述できるように。この「他には何もない」がこの記述を完成させる補完的言明である。しかし、これは度合いについての言明の分析としては適当でない。というのも、例えば明るさの単位をbとし、E(b )を実体 E がこの明るさを持つという言明としよう。すると、命題E(2b )は E が2倍の度合いの明るさを持つということを言う。この命題は E(b ) & E(b ) という論理積に分析可能なはずだが、しかしこの論理積は E(b ) と [論理的に] 同値である[4]。他方、単位の間に区別を設け、E(2b ) = E(b' ) & E(b'')と書くならば、明るさに異なる二つの単位を想定することになり、それゆえ、一つの実体が一つの単位 [だけ] を持つのなら、b' と b'' のうちどちらが [本当の] 単位なのかという問題が生じるが、こんな問題は明らかに馬鹿げている。
私の主張は、度合いを性質に帰属させる言明はそれ以上分析できず、さらに、度合いの相違という関係は内的関係であり、従ってそれは異なる度合いを帰属させる言明間の内的関係によって写像されるというものである。すなわち、原子命題はそれが帰属させる度合いと同じ多様性を持たなくてはならず、従って、数が原子命題の形式に含まれなければならないことが帰結する。度合いについての分析不可能な言明が相互に排除しあうということは、数年前に出版された私の著作 [=『論理哲学論考』] の「原子命題同士は互いに排除しあうことはできない」という見解と矛盾する。ここで私は慎重に「矛盾する」という語ではなく「排除する」という語を使っている。なぜなら、この二つの概念は異なるもので、原子命題は矛盾しえないが排除しあうことはありうるからだ。今からこの点を説明しよう。変項の一つの値に対してのみ真な命題を与えられるような諸関数が存在する。なぜなら――こういってかまわないだろう――その諸関数には一つの値に対しての余地しかないからだ。例えば、色 R が視野の特定の場所Pに特定の時刻 T において存在することを表明する命題を「RPT」と書くとする。とりあえず、そうした言明をさらに分析可能する方法については考えないことにする。すると [同様に] 、「BPT」は、色 B が視野の特定の場所 P に特定の時刻Tにおいて存在することを述べる。このとき、「RPT & BPT」は(単に偽な命題であるだけでなく)ある種の矛盾であることは、ここにいる大多数の人、そして日常生活においては全ての人にとって明らかであろう。さて、もし度合いについての言明が――私が以前考えていたように―― [さらに] 分析可能だとすれば、「色 R は R の全ての度合いを含み B の度合いは一切含まず、色 B は B の全ての度合いを含み R の度合いは一切含まない」と言うことによってこの矛盾を説明できるであろう。しかし上で述べたことから、度合いについての言明を排除できる分析などないということが帰結するのである。それでは、RPT と BPT の相互排除はどのような影響を及ぼすのか? 私の信じるところでは、相互排除は、RPT と BPT が共にある意味で完全であるという事実に存している。現実において関数「()PT」に対応するものは、ただ一つの実体に対する余地だけを残している。ちょうど、事実、私たちが「一つの椅子には一人の人間のためだけの余地しかない」と言うのと同じ意味において。私たちの記号表現は「RPT」と「BPT」の論理積の記号を作ることを許しており、その点において、現実の正しい像を与えていない。
私はどこかで命題は「現実に到達する」と述べた[5]。これによって私が意味していたのは、諸実体の形式は当の実体についての命題の形式に含まれているということである。というのも、文は、現実を当の文に投影する投影様式と一緒になって、ちょうど平面IIの像の比喩において、像が投影様式と一緒になって平面Iの図形の形を決定するのと同じように、実体の論理形式を決定するからである。この言明は、私の信じるところ、RPT と BPT の相互排除を説明する鍵を与えてくれる。なぜなら、命題が当の実体の論理形式を含むのであれば、二つの命題はまさにこの形式において衝突することがありうるからである。「今ブラウンがこの椅子に座っている」と「今ジョーンズがこの椅子に座っている」という命題は、それぞれある意味において、主語項をこの椅子に座らせようとしている。しかしこの二つの命題の論理積は両者を同時に同じ場所に座らせようとするため、衝突、つまり二つの項の相互排除を生じさせる。この排除自身は、記号表現においてどのように現れるだろうか? [一般に] 二つの命題 p, q の論理積は次のように書ける――
| p | q | |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
もしこの二つの命題が RPT と BPT だとするとどうなるだろう? その場合、一行目の「T T T」は消えなくてはならない[6]。この行は [現実には] 不可能な結合を写像しているからだ。真の可能性は次のようになる。
| RPT | BPT |
|---|---|
| T | F |
| F | T |
| F | F |
すなわち、第一の意味における RPT と BPT の論理積は存在しない[7]。そしてここにおいて、矛盾に対比する意味での排除が存在している。矛盾は、もし存在するとしたらだが、 [無理やり] 次のように書かねばなるまい。
| RPT | BPT | |
|---|---|---|
| T | T | F |
| T | F | F |
| F | T | F |
| F | F | F |
しかしこの表は無意義である。なぜなら、一行目の「T T F」がこの命題に、現実の可能性より多い論理的可能性を与えているからである。もちろん、このような無意義な構成を行うことを防げないのは、私たちの表記法の欠陥である。完全な表記法は、構文論の明確な規則によってこのような構造を排除せねばならない。その規則は、確定的な記号の図式によって記述されたある種の原子命題の場合は、特定の T と F の組み合わせを除外しなくてはらないことを私たちに教えるものでなくてはならない。しかしながら、問題となっている現象の究極的な分析に実際に到達しない限り、無意義な構造を排除する規則は手に入らないであろう。そして周知のように、その目的はまだ達成されていない。
訳註
[1] このsenseを意義と訳すか意味と訳すか、悩みました。というのも、ウィトゲンシュタインは『論考』では語に意義を認めていなかったため、この論文でもその立場を継承しているのではと思う一方、すぐ後のnonsensicalは明らかに「無意義な」と訳せるからです。結局、senseを「意義」、nonsensicalを「無意義な」と訳すことにしました。
[2] これは『論考』と同一の見解です。以下の節を参照。
命題は要素命題の真理関数である。
(『論考』5)
[3] 原子命題は『論考』における要素命題と同義の用語です。
[4] E(b) & E(b)の真理表を書くと、下表のようになります。これから分かるように、E(b)とE(b) & E(b)は論理的に同値です。一般に A ∧ A は巾等律と呼ばれ、A と同値な論理式の一つです。
| E(b) | E(b) | E(b) & E(b) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
ウィトゲンシュタインがこの段落で言おうとしていることは、性質の度合いを述べる命題、例えば「この紐は2メートルの長さだ」とか「今日の温度は15度だ」などの命題を、かつて自分はさらに分析可能だと考えいたが、それは誤りであった、ということです。その間違った分析の方法というのが、「この紐は2メートルの長さだ」という命題を「この紐は1メートルの長さである、かつ、この紐は1メートルの長さである」という真理関数によって表すことです。しかし「この紐は1メートルの長さである、かつ、この紐は1メートルの長さである」は、結局「この紐は1メートルの長さである」と同じことを述べているに過ぎません。
[5] 「像は現実と結び付けられている。像は現実に到達する。」(『論考』2.1511)
[6] なぜ1行目の「T T T」が消えなくてはならないかと言うと、「この点は赤い」を p、「この点は青い」を q とするなら、p と q が双方とも真であるような組み合わせは現実には存在しないからです。「赤であり、かつ、青であるような点」など考えられません。
このことから、色や音に関する感覚与件命題は相互に独立ではなく、従ってこれらの命題は要素命題ではないか、それとも要素命題同士も両立不可能でありうる、というどちらかを選ばなければなりません。
もし「これは赤い」という命題が要素命題ではなく、つまり複合命題であるなら、要素命題へ分析が可能なはずです。しかしこれ以上どうやっても分析のしようがあるようには思われません。かつて『論考』6・3751節で示唆されていた「色の粒子の配置」に訴えるアイデアでも問題は解決しません。すると結局、「二つの要素命題は独立不可能でありうる」(『哲学的考察』第76節)という結論を受け入れるほかありません。ここに、『論考』を支えるドグマの一つ「要素命題の独立性」が崩れることになります。
ただし、一点注意が必要ですが、これで要素命題そのものの存在が否定されたわけではありません。実際、ウィトゲンシュタインも、要素命題の存在を要請すること自体は正しいという考えを、これ以後も相変わらず保持していました。以下の文章を参照。
私は以前要素命題に関して二つの考えを抱いていた。一つは正しいと思われるが、もう一つは完全に間違っていた。第一の仮定は次のとおりである。私たちは命題の分析によって、最終的には、対象の直接的結合を表す命題に到達しなければならない。そこでは論理定項は役に立たない。というのも、「ではない」「かつ」「または」「もし …… ならば」は対象を結合するものではないからである。この第一の仮定は今でも揺らいでいない。第二に、要素命題は相互に独立でなければならないという考えを私は抱いていた。(中略)ここにおいて私は誤まっていた。
(『ウィトゲンシュタインとウィーン学団』1930年1月2日)
[7] 「第一の意味における論理積」とは通常の意味における論理積です。通常、二つの命題の論理積は、4行の真理表によって表現されますが、RPT と BPT の論理積の真理表には、見てのとおり3行しかありません。
著:L.ウィトゲンシュタイン 1929
訳:ミック
作成日:2003/12/25
最終更新日:2017/06/22

この 作品 は クリエイティブ・コモンズ 表示 4.0 国際 ライセンスの下に提供されています。

 Tweet
Tweet