集合で考える ―― HAVING句の力：その２

(DBAzine (2005/09/08), "Thinking in Aggregates")

帰ってきた HAVING句

　この記事は、「SQLで考える」の続編です。一応、セルコは両方の記事を独立に扱っていて、前作を読まなくても理解に支障はありませんが、タイトルも意識しているし、テーマも同じです。そのテーマとはすなわち、HAVING句の使い方を学ぶことによって、SQL の集合指向的な特徴を理解すること、です。今回はさらに核心へ踏み込んで、HAVING句が集合の性質を調べるためにどれほどの活躍を見せるかが明らかになります。

集合の性質

　私たちにとって集合という概念は、日常的に使う馴染み深いものです。りんご、バナナ、みかんをまとめて、{ りんご, バナナ, みかん } という一つの集合として扱う、というような「まとめ」操作は毎日やっています。しかし、人間の頭が簡単に扱う概念を数学が扱えるようになるまでには、長い時間を要しました。集合が数学の対象としてようやく認められたのは19世紀も末、ドイツの数学者カントールが集合論を創始したときでした（しかもすぐに認められることはなく、彼の苦悩は精神病院で死ぬまで続きます）。
　集合といっても、それは無関係な物の寄せ集めではありません。集合を作るときには、まとめるための基準なり条件が重要になります。さっきの例でいえば、「果物」という共通の性質を条件に作られています。共通性質がない雑多な集合を作ったところで、大して役に立ちません。むしろ、そういう共通性質を「集合」と名づけてもいいぐらいです。私たちも日常、意識するとしないとにかかわらず、集合を作るときは何らかの基準に従ってやっています。
　SQL では、GROUP BY句を使って、テーブルからいろいろな集合を作ることができますが、その場合もやはり、作られた集合の個々の要素の性質は問題ではなく、集合が全体としてどういう性質を持っているかが重要な場合が多くあります。

WHERE句と HAVING句の違い

　集合の性質を調べるといっても、そんなことどうやってやるの、と思われるかもしれません。ですが心配はいりません。そこで登場するのが HAVING句です。HAVING句は、行ではなく集合の性質を調べるために用意された道具です。特に、集約関数と極値関数と組み合わせたときの記述力には目を見張るものがあります。論より証拠、下の一覧表を見てください。

**【集合の性質を調べるための HAVING句の使い方一覧】**
1	HAVING COUNT (DISTINCT col_x) = COUNT (col_x)	col_x の値が一意である。
2	HAVING COUNT(*) = COUNT(col_x)	col_x に NULL が存在しない
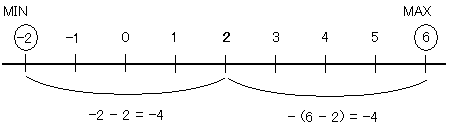
3	HAVING MIN(col_x - 定数) = - MAX(col_x - 定数)	col_x の最大値と最小値が指定した定数から同じ幅の距離にある
4	HAVING MIN(col_x) = - MAX(col_x)	col_x の最大値と最小値がゼロから同じ距離にある
5	HAVING MIN(col_x) * MAX(col_x) < 0	最大値の符号が正で最小値の符号が負
6	HAVING MIN(col_x) * MAX(col_x) = 0	最大値と最小値の少なくともどちらかがゼロ
7	HAVING MIN(col_x) * MAX(col_x) > 0	全ての col_x の符号が同じ
8	HAVING MIN(SIGN(col_x)) = MAX(SIGN(col_x))	col_x の全ての値が全て正、または全て負、または全てゼロである
9	HAVING MIN(ABS(col_x)) = 0	col_x は少なくとも一つのゼロを含む
10	HAVING MIN(ABS(col_x)) = MIN(col_x)	col_x はゼロ以上である（ただし、WHERE句でも同じ条件は書ける）
11	HAVING MIN(col_x) = MAX(col_x)	col_x は一つだけの値を持つか、または NULL である

　幾つか、補足説明を加えておきましょう。２番の「NULL の存在チェック」に COUNT(*) と COUNT(列名) を使うのトリックは、「SQLで考える」でも登場したので、お馴染みと思います。おさらいしておくと、COUNT(*) は NULL を数えるが、COUNT(列名) はそうではないという特性を利用しています。
　３番は、定数に平均を使えば、統計でいう偏差（deviation）の概念になると思えば分かりやすいでしょう。偏差とは、個々のデータから平均値を引いたものです。最小値と最大値が同じ偏差を持つということは、例えば下の数直線のように表せます。

　４番も、定数が偶然 0 だった場合だと考えれば、３番のヴァリエーションであることが分かります。
　８番は、SIGN関数を利用しています。これは数値の符号を調べる関数です。引数が正なら 1 を、0 なら 0 を、負なら -1 を返します。その最大値と最小値が一致するということは、集合内の全ての col_x の符号が同じだったということです。
　９番は、ABS関数を利用しています。これは絶対値（absolute value）を求める関数です。どんな数字の絶対値も 0 以上にしかなりませんから、もし絶対値の最小値が 0 だったとすれば、その集合の col_x には 0 が含まれていたことが分かります。

　こうした HAVING句の条件設定の特徴は、同じく条件設定の機能を持つWHERE句と対比するとよく分かります。WHERE句が行に対する条件を設定するのに対し、HAVING句は行集合に対する条件を設定します。

　　　　　　　WHERE句は「～であるような行」を検索する条件を設定する。
　　　　　　　HAVING句は「～であるような集合」を検索する条件を設定する。

　複数行をまとめて操作するこの力を持つがゆえに、HAVING句は集合指向言語に欠かさざる、重要な脇役であることが、理解していただけたでしょうか。

例題：歯抜けを探せ

　それでは今度は、具体的な例題を通して HAVING句を使ってみましょう。この例題もまた、手続き型言語と集合指向言語の発想の違いを浮き彫りにする好例です。それは、数列の歯抜けを探すというものです。次のテーブルを見てください。

**Foobar**
連番 (seq_nbr)	名前 (name)

1	トム
2	ディック
4	ハリー
5	モー

　「連番」という列名なのに、このテーブルでは数が連続していません。3 が歯抜けになっています。最初の課題は、このテーブルに歯抜けが存在するか否かをチェックすることです。この例のようにたかが4行なら一目瞭然ですが、100万行を目でチェックする猛者はいないでしょう。
　こういうとき、手続き型言語の考え方に慣れ親しんだ人は、ソートして一行づつ次の行と比較する、という方法を考えがちですが･･････この発想が御法度であることは、前作から読んでいただいた読者には、既に明らかと思います。そんなことをしたら、またセルコの叱責が飛びます。正しい道は、テーブル（集合）全体を一まとめにして考えること。そうすれば、歯抜けがなければ、行数と連番の最大値が一致しなければならない、という条件が見抜けます。ここまでくれば HAVING句の出番です。次のように書きます。

　　-- 行が返れば歯抜けあり
　　SELECT COUNT(*)
　　　FROM Foobar
　　HAVING COUNT(*) <> MAX(seq);

　このクエリの結果が一行でも返れば、歯抜けあり、一行も返らなければ歯抜けなしです。COUNT(*) で数えた行数と、連番の最大値が一致したなら、それは最初から最後まで歯抜けなくカウントアップできたという証拠だからです。歯抜けがあれば、COUNT(*) が MAX(seq) より小さくなり、HAVING句の条件が真になります。わずか3行のエレガントな解答です。手続き型言語で書いたときには、こう単純にはいきません。
　ところで、この SQL には GROUP BY句が存在しません。そのため、テーブル全体を一つの集合にまとめています。その場合でも、HAVING句は問題なく使用できます。時々、HAVING句は GROUP BY句と併用しなければならないと勘違いされていることがありますが、そういう訳ではないので注意してください。
　さて、これでこのテーブルに歯抜けが存在することが分かりました。今度は、この歯抜けを埋めるために、歯抜けになっている数値の最小値を求めます。「最小値」と来たら MIN関数。というわけで次のように書きます。

　　-- 歯抜けの最小値を探す
　　SELECT MIN(seq_nbr + 1)
　　　FROM Foobar
　　WHERE (seq_nbr + 1) NOT IN ( SELECT seq_nbr
　　　　　　　　　　　　　　　　　　　　　　　FROM Foobar);

　結果：
　MIN(seq_nbr + 1)
　-------------
　　　　　　　　　 3

　これもわずか4行。WHERE句の NOT IN を使ったサブクエリがどういう条件か、お分かりでしょうか？これは、ある連番について、それより一つ大きい数値がテーブル内に存在するかどうかを調べています。すると、（2、'ディック'）の場合だけ、次の 3 が見つからないため、条件が真になります。テーブルはファイルではないので、行に順序がありません。そのため、こういう比較のときにもソートをしません。この「ファイル VS テーブル」というのも、「手続き VS 集合」の局地戦の一つです。
　ところで余談ですが、この Foobar テーブルに「連番」列が NULL の行が存在した場合、このクエリの結果はとんでもないことになります。その場合は、NOT EXISTS を使って書き換える必要があります。どうとんでもないかすぐにピンと来なかった方、危険ですよ。このまますぐに「3値論理」へ飛んで、よく読んでください。

まとめ

　以上、2回にわたって、普通あまり重視されていない HAVING句の真価を解説してきました。一言で言うなら、HAVING句の真価は、集合に対して条件を設定できることです。この特徴を理解する一番いい方法は、誰でも知ってる WHERE句の機能と対比させることです。行ではなく行「集合」の視点からプログラミングを考えることが肝心です。
　そして、集約関数、極値関数、CASE式、サブクエリといった SQL が持つ強力な武器と組み合わせることで、HAVING句の力も相乗効果的に増大します。こうした武器を使いこなしていくことで、集合指向言語としての SQL が持つ豊かさ ―― それは決して手続き型言語やオブジェクト指向言語に劣るものではありません ―― もますます明らかになっていくでしょう。
　ちょっと楽しくなってきんじゃあ、ありませんか。

戻る