ホーム > リレーショナル・データベースの世界 >
SQLで木と階層構造のデータを扱う(2)―― 経路列挙モデル
「SQL で木構造のデータを扱う」第二回です。前回は、入れ子集合モデルという独創的な、しかしまだ実験段階にとどまる新しい方法論を紹介しました。今回は、もう一つ新たなモデルを見ていきましょう。新しい、といってもやっぱりこれもアイデア自体は古くからあるもので、歴史自体は入れ子集合モデルより遡ります。名前は「経路列挙モデル(Path Emuneration Model)」(または「経路実体化モデル(Materialized Path Model)」)。むしろ、ファイル管理のモデルとしてはお馴染みのものですが、データベースのモデリング方法として注目を集めたのは、2000年に刊行された I.ベンガンと T.モローの共著『Advanced Transact-SQL for SQL Server 2000』によるところが大きいと言われています。
このモデルもまた、それ自身非常にエレガントで見事なものです。特に検索クエリの簡素化と効率化に絶大な威力を発揮します。一方で、入れ子集合モデルとよく似たところも持っていて、両者を対比しながら考えると、面白さも倍増すること請け合いです。
それでは、早速はじめましょう。
木構造は、多くの面白い特性を備えていますが、そのうちの一つに、「ルートから各ノードまでのパスが必ず一つあり、かつ一つしかない」というものがあります。子が複数の親に属するネットワーク構造や、リーフがルートに循環する円環構造には、こういう特性はありません。
これを集合論の言葉で表現すると、「ノードとパスには一対一対応(全単射)が存在する」ということです。従って、一ノードを一行で表現するテーブルを作れば、パスを直接データとして保存することが可能になります。前回、入れ子集合モデルでは、ノードを円に見立てて座標の大小によって包含関係を記述しました。それに倣って言えば、今回の経路列挙モデルの要諦はこうです。
ノードをディレクトリ(フォルダ)と見なし、各ノードがルートからのパス情報を保持すると考える
「ノードがディレクトリ? 何言ってるんだ?」と思うかもしれませんが、論より証拠、図示してみれば、すぐに「なあんだ」と思うでしょう。木構造のデータ・サンプルには、前回と同じく次のような組織図を例に取りましょう。
図1-1. ノードをディレクトリに見立てる
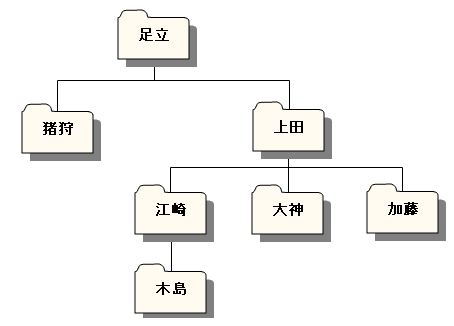
いかがでしょう。ノードがディレクトリに見えてきましたか? では、テーブルも作りましょう。
--経路列挙モデルによる木構造の表現
CREATE TABLE OrgChart
(emp VARCHAR(32) PRIMARY KEY
CHECK (REPLACE(emp, '/', '') = emp),
path VARCHAR(256) NOT NULL,
UNIQUE (path));
--パスを主キーで表す場合
DELETE FROM OrgChart;
INSERT INTO OrgChart VALUES ('足立', '/足立/');
INSERT INTO OrgChart VALUES ('猪狩', '/足立/猪狩/');
INSERT INTO OrgChart VALUES ('上田', '/足立/上田/');
INSERT INTO OrgChart VALUES ('江崎', '/足立/上田/江崎/');
INSERT INTO OrgChart VALUES ('木島', '/足立/上田/江崎/木島/' );
INSERT INTO OrgChart VALUES ('大神', '/足立/上田/大神/' );
INSERT INTO OrgChart VALUES ('加藤', '/足立/上田/加藤/' );
--パスを番号で表す場合
DELETE FROM OrgChart;
INSERT INTO OrgChart VALUES ('足立', '.1.');
INSERT INTO OrgChart VALUES ('猪狩', '.1.1.');
INSERT INTO OrgChart VALUES ('上田', '.1.2.');
INSERT INTO OrgChart VALUES ('江崎', '.1.2.1.');
INSERT INTO OrgChart VALUES ('木島', '.1.2.1.1.' );
INSERT INTO OrgChart VALUES ('大神', '.1.2.2.' );
INSERT INTO OrgChart VALUES ('加藤', '.1.2.3.' );
一行が一人の社員(ノード)を表すことは、入れ子集合モデルや隣接リストモデルと同じです。特徴は、なんと言っても path 列にあります。要するに、各ノードまでの絶対パスをデータとして保存しているのです。主キーを使う表現と番号を使う表現(よく書籍の章立てなんかで見る形式ですね)の二つがありますが、特に、区切り文字に「/」を使っている前者に注目してください。まさに UNIX のファイルシステムの構造そのものではありませんか(Windows を使い慣れている人は「\」マークに置き換えて考えてください)。ファイルシステムも木構造なのだから、同じなのは当然といえば当然なんですけど、まさに「コロンブスの卵」です。チェック制約は、「社員の名前に区切り文字を含んではならない」という禁則です。
入れ子集合モデルでは、円の包含関係で階層を表現したのに対し、今度はパス文字列の包含関係で表現しています。面白いことに今回の場合、子供のパスが親のパスを含むという、入れ子集合とは反対の包含関係になっています。例えば、加藤氏の「足立/上田/加藤」というパスは、その親である上田氏の「足立/上田」や足立氏の「足立」といったパスを含みます。ルートのパスは全てのノードのパスの部分集合になっています。子は先祖たちの膨大な情報を受け継いでいく存在なのです。
ノード自身のレコードに親子関係が含まれているので、他のモデルに比べて経路探索のクエリが圧倒的に簡単になります。特に、PostgreSQL や Oracle(10g以降)のように正規表現を利用できる DB と極めて高い親和性を示します。パフォーマンス面においても、先述のように、path もテーブル上で一意になるため、一意制約を付けることが可能です。反対に欠点は、ざっと以下に挙げるとおりです。
- パスに主キーを使うと、パス文字列が非常に巨大になる危険がある。番号を使えば、この心配は少ない。
- パスに主キーを使うと、同じ階層内のノード同士の順序が一般的に把握できない(入れ子集合モデルでは、ノードの座標位置で示すことができた)。やはり番号を使うことで、この欠点も補える。
- しかし、パスに番号を使うと、ノードの削除、追加などの更新が非常に難しい。
- 検索条件で文字列操作を多用するため、文字列関数の標準化が遅れている SQL では、かなり実装依存のコードになってしまう(もっとも、これをモデルの欠点と言うのはかわいそうで、むしろ SQL の欠点と言うべきですが)。
総じて言えば、更新が少なく、大量データの検索が必要なケース(例えばデータウェアハウス)に向いているモデルです。以下で見ていく SQL は、基本的に主キーと番号のどちらのケースにも対応できるものを紹介します。両者で別々のクエリを使う必要がある場合、またはどちらかでは不可能なケースについては、そのつど注意を促します。
なお、どちらの方法でも区切り文字は必須なので、面倒がらずに付けましょう。区切り文字がないと、例えば「上田山野井」というパスが「上田/山野井」なのか「上田山/野井」なのか、あるいは「111」が「1.11」なのか「1.1.1」なのか区別つきません。また、パスの先頭と終端は必ず区切り文字で囲んでください。些細なことに見えるかもしれませんが、これを囲むと囲まないとでは、更新クエリの効率に大きな違いが出るのです(UNIX のパスが /home/usr/bin/ のように区切り文字で囲まれているのも、きっと同じ理由によるのだと思います)。
さて、テーブルを作ったら、まずは検索から始めましょう。木のルートとリーフを探す簡単な方法から、ノード同士の階層関係を調べる方法など、いずれも階層データを扱うために必要不可欠の操作ばかりです。
まず、基本となるの操作は、ルート(根)とリーフ(葉)を探すことです。ルートは親を持たないノードのことで、木構造には一つしか存在しえまえせん。この組織図で言えば社長の足立氏がそうです。一方、リーフはその反対で、子を持たないノードのことで、猪狩、木島、大神、加藤の四氏です。
経路列挙モデルでルートを求めることはとても簡単です。番号を 1 番から使っていれば、ずばり path = '1' のノードなので、
--ルートを求める:パスが番号の場合
SELECT *
FROM OrgChart
WHERE path = '.1.';
emp path
----- -----
足立 .1.
パスに主キーを使っている場合は「区切り文字を削除した文字列がキーと同じになる」という条件にしましょう。
--ルートを求める:パスが主キーの場合
SELECT *
FROM OrgChart
WHERE emp = REPLACE(path, '/', '');
emp path
----- -----
足立 /足立/
REPLACE はほとんどの DB で使える標準関数です。左辺を emp 列にしておくのは、もちろんインデックスを利用できるようにするための小技です。
一方、リーフを求めるクエリは、ちょっと考える必要があります。リーフである猪狩、木島、大神、加藤の四氏と、そうでない足立、上田氏らを比べてみてください。リーフ・ノードが共通して持ち、そうでないノードが持たない性質が見えてこないでしょうか。それは何かと言うと、
自分のパスの後ろに追加のパスを持つようなノードが存在しない
という性質。例えば、リーフでない上田氏のパス「/足立/上田/」について見ると、「/足立/上田/江崎/」(江崎)、「/足立/上田/加藤/」(加藤)のように、「自分のパス + 追加のパス」を自らのパスとするようなノードが存在します。リーフの人々は、こういうノードを持ちません。自分で打ち止めです(それがリーフの定義なのだから当然ですけど)。そこで、この条件を NOT EXISTS で表しましょう。
--リーフを求める
SELECT *
FROM OrgChart Parents
WHERE NOT EXISTS
(SELECT *
FROM OrgChart Children
WHERE Children.path LIKE Parents.path || '_%');
emp path
------ ----------------------
猪狩 /足立/猪狩/
木島 /足立/上田/江崎/木島/
大神 /足立/上田/大神/
加藤 /足立/上田/加藤/
「'_%'」は、「(一文字以上の)任意の文字列」を意味するパターンです。LIKE は前方一致検索においてはインデックスを使用するので、パフォーマンスも良好です。文字列を結合する || 演算子はれっきとした標準関数ですが、やはり実装に左右されます。Oracle、PostgreSQL、DB2 では問題なく使えますが、SQLServer では「+」、MySQL では CONCAT を使う必要があります。
木の中で、あるノードの深さ、つまりレベルは、ルートとそのノードの間に存在するパス(経路)の数になります。パスは、図でいえばノード同士を結び付けている線に相当します。レベルの数値が大きくなればなるほど、そのノードはルートから遠くに位置することになります。
経路列挙モデルでは、パスを直接データとして保存しているので、深さを求めるのは非常に簡単です。区切り文字の数を数えてやれば、0 を開始値とする深さになりますし、数字の数を数えれば 1 を開始値とする深さになります。
区切り文字の数を数えるには、「(元の文字列長) - (区切り文字を削除した文字列長)」という引き算で可能です。例えば、「/足立/上田/大神/」(長さ=10)から「足立上田大神」(長さ=6)を引けば、区切り文字の数が求められます。後は「両端に植木がある場合」の簡単な植木算です。
--ノードの深さを計算する
SELECT emp, LENGTH(path) - LENGTH(REPLACE(path, '/', '')) -1 AS lvl
FROM OrgChart;
emp lvl
------ -----
足立 1
上田 2
猪狩 2
江崎 3
加藤 3
大神 3
木島 4
入れ子集合モデルに比べると実に簡潔なクエリで可能なことがお分かりいただけるでしょう。LENGTH は、SQLServer では LEN に置き換えてください。
これはさっきの問題の応用です。木の全体の高さを求めるには、さっき出したノードの深さの一覧の中から、最大値を選択すればよいわけです。
--木の高さを計算する
SELECT MAX(LENGTH(path) - LENGTH(REPLACE(path, '/', '')) -1) AS height
FROM OrgChart;
height
-------
4
簡単でしょう? そろそろこのモデルの魅力が分かり始めたんじゃないでしょうか?
ノードの深さがすぐに分かるということは、ノードの位置する階層を視覚的に表現するのもお手の物ということ。
--階層をインデントで表現する
SELECT LPAD(emp, LENGTH(path) - LENGTH(REPLACE(path, '/', '')) , ' ') AS emp
FROM OrgChart;
emp
--------------
足立
猪狩
上田
江崎
木島
大神
加藤
なお、LPAD は Oracle、PostgreSQL、MySQL でのみ使用可能です。DB2 では REPEAT、SQLServer では REPLICATE 関数で代用します。
子供から見て直属の親とは、自分のパスに含まれる上層の人々のうち最大のパスを持つノードということです。従って、入れ子集合モデルと全く同じ考え方で求められます。子供のノードを持たない猪狩、大神などの人々の worker 列には NULL が現れます。
--親から見た場合の子供
SELECT Boss.emp AS boss, Worker.emp AS emp
FROM OrgChart Boss
LEFT OUTER JOIN OrgChart Worker
ON Boss.path = (SELECT MAX(path)
FROM OrgChart
WHERE Worker.path LIKE path || '_%');
boss emp
------ ----
足立 猪狩
足立 上田
猪狩
上田 江崎
上田 大神
上田 加藤
江崎 木島
木島
大神
加藤
これは、外部結合の結合条件で相関サブクエリを使っています。子供のパスに含まれるパスを持つ上層のノードを求め、そのうちの最大のパスを持つのが直属の親である、という条件を記述しているのです。やはり LIKE の前方一致検索なので、パフォーマンスも申し分ない。上司が何人の直属の部下を従えているかも、このクエリの結果を集約すれば簡単に分かります。
--親の持つ子供の数
SELECT Boss.emp AS boss, COUNT(Worker.emp) AS cnt
FROM OrgChart Boss
LEFT OUTER JOIN OrgChart Worker
ON Boss.path = (SELECT MAX(path)
FROM OrgChart
WHERE Worker.path LIKE path || '_%')
GROUP BY Boss.emp;
boss cnt
----- ----
足立 2
猪狩 0
上田 3
江崎 1
大神 0
加藤 0
木島 0
子供の数を数えるのには、入れ子集合モデルのときと同様、COUNT(*) ではなく COUNT(列名) を使いましょう。反対に子供を主軸に見たい場合は、子供を主とした外部結合に反転させるだけ。次のクエリで OK。
--子から見た場合の親
SELECT Worker.emp AS emp, Boss.emp AS boss
FROM OrgChart Worker
LEFT OUTER JOIN OrgChart Boss
ON Worker.path > Boss.path
AND Boss.path = (SELECT MAX(path)
FROM OrgChart
WHERE Worker.path LIKE path || '_%');
emp boss
----- ------
足立
猪狩 足立
上田 足立
江崎 上田
大神 上田
加藤 上田
木島 江崎
今度は、上司を持たないのはルートの足立氏だけなので、足立氏の行の boss 列だけが NULL になります。本当は、結合条件の「Boss.lft < Worker.lft」は論理的には不要なのですが(事実、PostgreSQL ではなくてもいい)、Oracle ではこれがないと正しく動作しないため、安全のため入れておきます。おそらく、外部結合のマスタとなるテーブルの列を結合条件に使わねばならない、という独自仕様の(困った)ルールがあるのでしょう。
このクエリは応用がきいて、隣接リストモデルへの変換もこのクエリを利用して行うことができます。「3-8.経路列挙モデルから隣接リストモデルへ変換する」を参照。
木は再帰的構造です。だかr、一つの木の中には多くの小さな木が含まれています。そういう小さな木を「部分木」と言います。ちょうどある集合の中に含まれる集合を「部分集合」と言うのと同じですね。今度は、子供を持つノードについて、自分をルートとする部分木を列挙してみましょう。
--部分木を求める
SELECT Boss.emp AS boss, Worker.emp AS worker
FROM OrgChart Boss, OrgChart Worker
WHERE Worker.path LIKE Boss.path || '_%'
ORDER BY Boss.path;
boss worker
--------------
足立 猪狩
足立 上田
足立 江崎
足立 木島
足立 大神
足立 加藤
上田 江崎
上田 木島
上田 大神
上田 加藤
江崎 木島
子供は、パスの途中までは親と一致するため、LIKE で前方一致検索すればよいわけです。ルートとしたいノードが決まっているなら「Boss.emp = :boss_name」という条件を追加してパラメータで渡してあげましょう。自分も部分木に含めて表示したいなら「_%」の代わりに「%」を使えば OK。
ルートからあるノードまでのパスを、列持ちの形式で列挙してみましょう(行持ちの形式は次に見ます)。これも、入れ子集合モデルと同じ考え方でいけます。直属の親は、自分のパスに含まれるパスのうち最大のパスを持つノードでした。後は、「親の親」についても同じ考えで上層へ推移していけばいいわけです。
--パスを列挙する(列持ちバージョン):そのフ1
SELECT O1.emp,
(SELECT emp
FROM OrgChart
WHERE path = MAX(O2.path)) AS level_0,
(SELECT emp
FROM OrgChart
WHERE path = MAX(O3.path)) AS level_1,
(SELECT emp
FROM OrgChart
WHERE path = MAX(O4.path)) AS level_2
FROM OrgChart O1
LEFT OUTER JOIN OrgChart O2
ON O1.path LIKE O2.path || '_%'
LEFT OUTER JOIN OrgChart O3
ON O2.path LIKE O3.path || '_%'
LEFT OUTER JOIN OrgChart O4
ON O3.path LIKE O4.path || '_%'
GROUP BY O1.emp;
emp level_0 level_1 level_2
---------------------------------
足立
猪狩 足立
上田 足立
江崎 上田 足立
大神 上田 足立
加藤 上田 足立
木島 江崎 上田 足立
やはりスカラ・サブクエリ内の MAX 関数の使用が目を引きますね。このラディカルなクエリが動作しない保守的な DB では、次の別解を使いましょう。
--パスを列挙する(列持ちバージョン):そのフ2
SELECT O0.emp, O1.emp AS level_1, O2.emp AS level_2, O3.emp AS level_3
FROM OrgChart O0
LEFT OUTER JOIN OrgChart O1
ON O1.path = (SELECT MAX(path)
FROM OrgChart
WHERE O1.path LIKE O0.path || '_%')
LEFT OUTER JOIN OrgChart O2
ON O2.path = (SELECT MAX(path)
FROM OrgChart
WHERE O2.path LIKE O1.path || '_%')
LEFT OUTER JOIN OrgChart O3
ON O3.path = (SELECT MAX(path)
FROM OrgChart
WHERE O3.path LIKE O2.path || '_%');
もっと簡単な方法として、正規表現を使う方法もあるかもしれません。パス列にはルートから各ノードまでの絶対パスが保存されているので、あとはこのパスを区切り文字ごとに分割してやればいいわけです(ホスト言語側で文字列関数を使うのが一番簡単かもしれませんが)。
いま、最初から二つのノードが与えられていた場合、そのノードをつなぐパスを表示することを考えます。2-7 では列持ちで結果を表示しましたが、今度は行持ちにします。
これは、次のように始点ノード(O1)と終点ノード(O2)に挟まれる中間ノード(O2)を求めることで可能です。path 列は、ノードをソートする際にも使えます。
--ノード間のパスを検索する
SELECT O1.emp, O1.path
FROM OrgChart O1, OrgChart O2
WHERE O1.path >= (SELECT path FROM OrgChart WHERE emp = :start_node)
AND O2.emp = :end_node
AND O2.path LIKE O1.path || '%'
ORDER BY O1.path;
それともうひとつ、このクエリを使うときには一つ注意点があります。それは、一度レベルを上に上がらないと辿り着けないような検索ができないことです。例えば、加藤氏と木島氏をつなぐパスは「加藤 - 上田 - 江崎 - 木島」ですが、「加藤 → 上田」で上層に移動する必要があるため、うまくいきません。言い換えると、単調下降(というか単調上昇というか)のケースでしか動きません。
--単調下降の場合はOK
SELECT O1.emp, O1.path
FROM OrgChart O1, OrgChart O2
WHERE O1.path >= (SELECT path FROM OrgChart WHERE emp = '足立')
AND O2.emp = '木島'
AND O2.path LIKE O1.path || '%'
ORDER BY O1.path;
emp path
----- -------------------
足立 /足立
上田 /足立/上田
江崎 /足立/上田/江崎
木島 /足立/上田/江崎/木島
--上下移動が必要な場合はダメ
SELECT O1.emp, O1.path
FROM OrgChart O1, OrgChart O2
WHERE O1.path >= (SELECT path FROM OrgChart WHERE emp = '加藤')
AND O2.emp = '木島'
AND O2.path LIKE O1.path || '%'
ORDER BY O1.path;
(結果が不正)
emp path
------ ----------------------
江崎 /足立/上田/江崎/
木島 /足立/上田/江崎/木島/
では、このクエリを、上下移動する必要がある場合にも使えるように拡張する方法はあるでしょうか? 入れ子集合モデルの場合と同様、これもかなりの難問だと思います。腕に自信のある方、チャレンジしてみてください。
今度は、ノード間の関係を少し大雑把に分類してみましょう。つまり、二つのノードが、互いに親子の関係にあれば、そのように表示し、先ほどのように一度上昇せねば辿り着けない場合は「無関係」と表示しましょう。これは、パスの包含関係を調べればすぐに分かります。
--ノード同士の相対位置を表示する
SELECT CASE WHEN :first_node = :second_node
THEN :first_node || ' = ' || :second_node
WHEN O1.path LIKE O2.path || '_%'
THEN :first_node || ' は ' || :second_node || ' の部下'
WHEN O2.path LIKE O1.path || '_%'
THEN :second_node || ' は ' || :first_node || ' の部下'
ELSE :first_node || ' は ' || :second_node || ' と無関係' END AS rel_nodes
FROM OrgChart O1, OrgChart O2
WHERE O1.emp = :first_node
AND O2.emp = :second_node;
例えば、木島氏は上田氏をルートとする部分木に属するので、木島氏は上田氏の部下です。一方、江崎氏と加藤氏は、同じ階層なので上下関係はありません。よって「無関係」です(この際、個人的な交友はあったとしても無視します)。
--上田氏と木島氏の関係
SELECT CASE WHEN '上田' = '木島'
THEN '上田' || ' = ' || '木島'
WHEN O1.path LIKE O2.path || '_%'
THEN '上田' || ' は ' || '木島' || ' の部下'
WHEN O2.path LIKE O1.path || '_%'
THEN '木島' || ' は ' || '上田' || ' の部下'
ELSE '上田' || ' は ' || '木島' || ' と無関係' END AS rel_nodes
FROM OrgChart O1, OrgChart O2
WHERE O1.emp = '上田'
AND O2.emp = '木島';
rel_nodes
---------------------
木島 は 上田 の部下
--江崎氏と加藤氏の関係
SELECT CASE WHEN '江崎' = '加藤'
THEN '江崎' || ' = ' || '加藤'
WHEN O1.path LIKE O2.path || '_%'
THEN '江崎' || ' は ' || '加藤' || ' の部下'
WHEN O2.path LIKE O1.path || '_%'
THEN '加藤' || ' は ' || '江崎' || ' の部下'
ELSE '江崎' || ' は ' || '加藤' || ' と無関係' END AS rel_nodes
FROM OrgChart O1, OrgChart O2
WHERE O1.emp = '江崎'
AND O2.emp = '加藤';
rel_nodes
---------------------
江崎 は 加藤 と無関係
このクエリは、入れ子集合モデルのときの方法とよく似ていますね。入れ子集合モデルが円の包含関係によって階層を表現したのに対し、経路列挙モデルでは、文字列の包含関係によってそれを表現しています。
この章では、木やノードの追加・削除、あるいは木の中で動かしたりといった、木の形そのものをダイナミックに動かす方法について見ていきます。
木の中から、部分木をごっそり削除することを考えます。いまはサンプルに会社の組織図を使っているので、それに即して言えば、社員をクビにすることに相当します。しかも、その解雇対象の社員が部下を持っている場合は、哀れ彼らも連座して解雇されます。
まず、パスが主キーの場合は、次のように解雇対象の社員のパスを含む社員を全員削除することで可能です。
--部分木の削除
DELETE FROM OrgChart
WHERE path LIKE '%/' || :fired_emp || '/%';
例えば、江崎氏を解雇すると、連座して部下の木島氏も解雇されます。
--江崎氏を解雇(木島氏も連座)
DELETE FROM OrgChart
WHERE path LIKE '%/' || '江崎' || '/%';
--解雇後の組織図
emp path
----- -----------------
足立 /足立/
猪狩 /足立/猪狩/
上田 /足立/上田/
大神 /足立/上田/大神/
加藤 /足立/上田/加藤/
この方法の欠点は、中間一致検索のため、path 列のインデックスが利用できないこと、およびパスが番号の場合は使えないことです。この二点を改良したのが次の解です。
--部分木の削除:一般化
DELETE FROM OrgChart
WHERE path LIKE (SELECT path
FROM OrgChart
WHERE emp = :fired_emp) || '%';
これなら、path 列も emp 列もインデックスを利用できます。スカラ・サブクエリも非相関のうえ emp 列は主キーなので、パフォーマンスは非常に良好です。しかも、パスが番号でも問題なく使えるという汎用性の高さも兼ね備えた名答です。
図3-1. 部分木の削除(部下も連座)
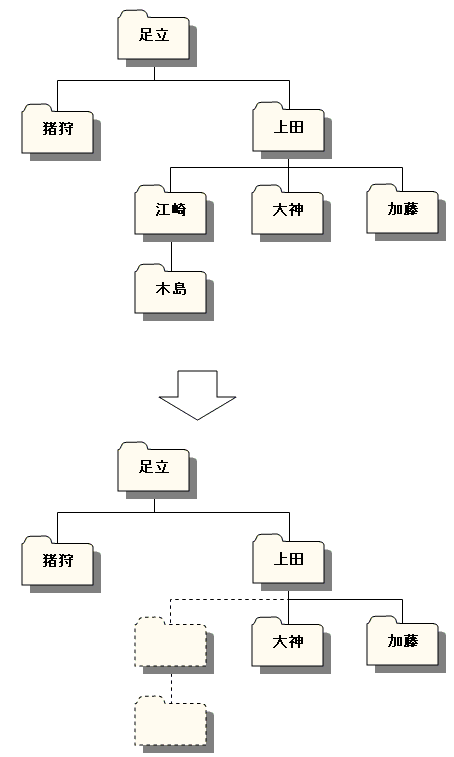
単一ノードの削除は、入れ子集合モデルに比べると難しい問題になります。特に、番号にパスを使った場合は、番号の振りなおしが必要になるため、一般的な解法を見つけるのは難しいでしょう。そのため以下では、パスに主キーを使うものとして話を進めます。
まず、削除したいノードが中に子供を持たないリーフであると分かっていれば、迷わずそのノードを削除するだけでかまいません。
--単一ノードの削除
DELETE FROM OrgChart
WHERE emp = :dead_emp;
一方、子供を持つ親ノードを削除する場合は、気をつけねばなりません。単純にそのノードを削除しただけだと、パスにまだ「幽霊」が残り、全体としてもはや木構造ではなくなってしまうからです。この幽霊に成仏してもらう方法は、入れ子集合のときと同様の二つです。孤児を祖父母が引き取るか、子供の一人を家長に昇格させるか。
祖父母が引き取るケースでは、二段階を踏んで、削除したノードをあらゆるパスから抹消してやればOKです。いわばダルマ落としのイメージで、「パスを詰める」わけですね。
--1.親ノードの削除
DELETE FROM OrgChart
WHERE emp = :dead_emp;
--2.パスを詰める
UPDATE OrgChart
SET path = REPLACE(path, '/' || :dead_emp || '/', '/')
WHERE path LIKE '%/' || :dead_emp || '/%';
例えば、上田氏が死んだ場合を考えると
--1.親の削除
DELETE FROM OrgChart
WHERE emp = '上田';
--パスに上田氏の幽霊が残り、木が崩れてしまワう
emp path
---- ----------------------
足立 /足立/
猪狩 /足立/猪狩/
江崎 /足立/上田/江崎/
木島 /足立/上田/江崎/木島/
大神 /足立/上田/大神/
加藤 /足立/上田/加藤/
--2.パスを詰める
UPDATE OrgChart
SET path = REPLACE(path, '/' || '上田' || '/', '/')
WHERE path LIKE '%/' || '上田' || '/%';
--無事成仏
emp path
----- -----------------
足立 /足立/
猪狩 /足立/猪狩/
江崎 /足立/江崎/
木島 /足立/江崎/木島/
大神 /足立/大神/
加藤 /足立/加藤/
2番目のクエリで中間一致検索に頼らざるをえないのが難点ですが、ロジックは非常に単純です。ただし、この方法だと、ルートを削除することはできないので注意してください。ルートより上の引き取り手はいないからです。また、パスに番号を使った場合、番号の再割り当てが難しいため、この方法では更新は難しいでしょう。
図3-2-1. 単一ノードの削除(孤児は祖父母が引き取る)
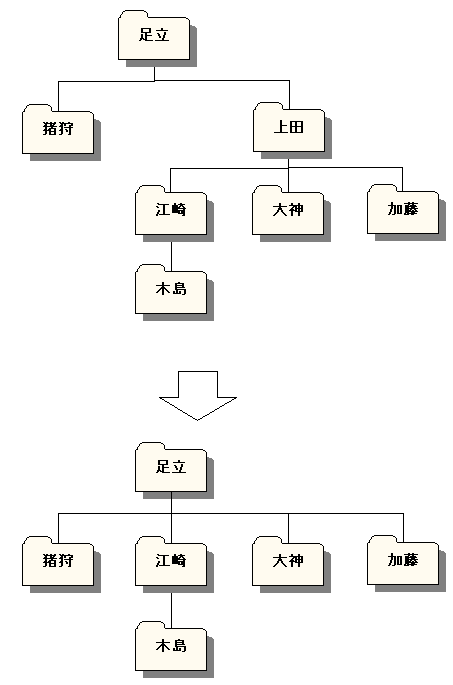
では今度は、親の死後、子供の一人に家長の権限を委譲するケースを考えましょう。この方法なら、ルートも削除できますが、複数の子供の誰を新たな「親」とするか、ルールを決める必要があります。とりあえず江崎氏に立ってもらうとしましょう。イメージは下図のようになります。
図3-2-2. 単一ノードの削除(子供の一人が上に立つ)
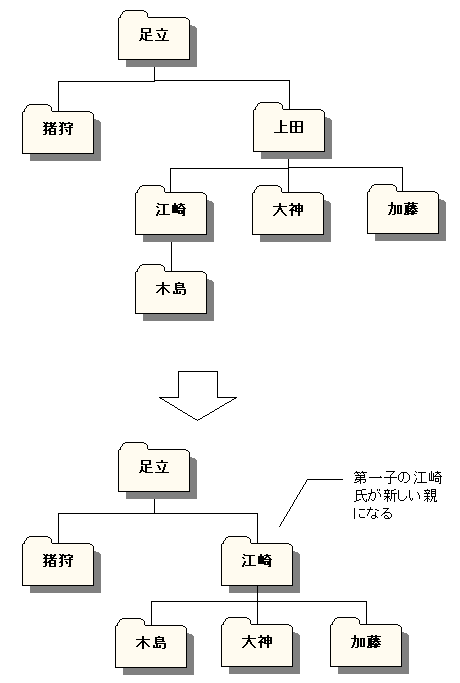
最初に削除対象の上田氏を削除する点は、先ほどと変わりません。後は、パス内で上田氏が占めていたポジションを、江崎氏で塗り替えてやればよいでしょう。
--1.親の削除
DELETE FROM OrgChart
WHERE emp = :dead_emp;
--2.パスを再編成
UPDATE OrgChart
SET path = REPLACE(REPLACE(path, '/' || :new_parent || '/', '/'),
'/' || :dead_emp || '/', '/' || :new_parent || '/')
WHERE path LIKE '%/' || :dead_emp || '/%';
文字列の置換を二回行っています。内側の置換が古い親を新しい親で塗り替え、外側の置換が、新しい親の元いたポジションを削除するものです。上田氏の跡目を江崎氏が継ぐ場合は、次のような動作になります。
--1.親の削除
DELETE FROM OrgChart
WHERE emp = '上田';
--パスに上田氏の幽霊が残り、木が崩れてしまワう
emp path
---- ----------------------
足立 /足立/
猪狩 /足立/猪狩/
江崎 /足立/上田/江崎/
木島 /足立/上田/江崎/木島/
大神 /足立/上田/大神/
加藤 /足立/上田/加藤/
--2.江崎氏を親に立ててパスを再編成
UPDATE OrgChart
SET path = REPLACE(REPLACE(path, '/' || '江崎' || '/', '/'),
'/' || '上田' || '/', '/' || '江崎' || '/')
WHERE path LIKE '%/' || '上田' || '/%';
emp path
----- ------------------
足立 /足立/
猪狩 /足立/猪狩/
江崎 /足立/江崎/
木島 /足立/江崎/木島/
大神 /足立/江崎/大神/
加藤 /足立/江崎/加藤/
もちろん、江崎氏以外の子供を立てることも同様に可能です。今度は、REPLACE を二度使ってパスを更新しています。処理の内訳は次のとおりです。
- 新しく親として立つ子供の名前を、現在のパス位置から削除する(内側の置換)
- 削除された親を新しい親の名前で書き換える(外側の置換)
ところで、冒頭で「パスを必ず区切り文字で囲っておくこと」という注意を促したのを覚えているでしょうか? 実は、ここでその配慮が生きてきます。というのも、例えば、もしパスの右端の区切り文字を省略した場合、新たに親となる江崎氏のパスは「/足立/上田/江崎」ですが、江崎氏にぶらさがる木島氏のパスは「/足立/江崎/木島」です。どちらも「江崎」を削除せねばなりませんが、REPLACE(path, '/' || '江崎' , '/') とすることはできません。前者のパスが「/足立/上田/」という違う形式に変わってしまうからです。
同様に、パスの左端の区切り文字を省略しても不都合が生じます。今度はどうなるかといえば、ルートを削除する場合と、それ以外のノードを削除する場合で WHERE 句の条件が変わってしまいます。そういう場合、ルート削除のときの条件は、「path LIKE '足立' || '/%'」という形になりますが、ルート以外のノードでは「path LIKE '%' || '上田' || '/%'」という形にせざるをえません。両端に区切り文字を付加することで、更新 SQL を一つの形に統一できるメリットがあるのです。
木にノードを追加するときは、リーフとして追加するのか、それとも親として追加するのかを決める必要があります。まずは、リーフの方から見ていきましょう。リーフを追加するには、どの親の配下に付けるかさえ分かれば、その親のパスに自分を追加するだけで OK です。パスに番号を使う場合も、基本的には同じです。
--リーフの新規追加
INSERT INTO OrgChart
VALUES (:new_emp, (SELECT path FROM OrgChart WHERE emp = :parent) || :new_emp || '/');
例えば、猪狩氏の配下に新たに国見氏を加えるとすれば、次のようになります。
INSERT INTO OrgChart
VALUES ('国見', (SELECT path FROM OrgChart WHERE emp = '猪狩') || '国見' || '/');
emp path
----- ---------------------
足立 /足立/
猪狩 /足立/猪狩/
上田 /足立/上田/
江崎 /足立/上田/江崎/
木島 /足立/上田/江崎/木島/
大神 /足立/上田/大神/
加藤 /足立/上田/加藤/
国見 /足立/猪狩/国見/ --新規ノード
もし親が既に子供を持っていた場合、本当なら何番目の子供として持つかを決める必要があります。しかし、主キーをパスに使うと、一般的に子供の間に順序をつけられません(キー自体が順番を示すなら別ですが)。従って、同じ階層のノード同士に序列を付けたいなら、必ずパスに番号を使って明示的に示す必要があります。円の座標位置によってノードの順序を暗示できる入れ子集合モデルと違って不便なところです。
既存のノードを含むような「親」として新たなノードを追加することを考えましょう。いわば、木の「中間」にぐいっと新しいノードを押し込んでやるのです。これは、単純に木の下端に追加するだけでよかったリーフよりも骨が折れます。新たに持つことになる子供の数だけ処理をループさせる必要があるため、多分 SQL 単独では解決できないでしょう。
まず第一段階は、当然ながら親の行を追加することです。この場合、「親」とは言っても、既存のノードのどれかに従属する「子」と同じですから、さっきのリーフ追加の SQL を実行しましょう。大事なのはその次で、新しい親の配下に従属させたいすべてのノードについて、パスを更新します。
--親の新規追加
INSERT INTO OrgChart
VALUES (:new_emp, (SELECT path FROM OrgChart WHERE emp = :parent) || :new_emp || '/');
--第二段階:パスの更新(必要なだけ繰り返すキ)
UPDATE OrgChart
SET path = REPLACE(path, '/' || :child || '/', '/' || :new_parent || '/' || :child || '/')
WHERE path LIKE '%/' || :child || '/%';
例えば、大神氏と加藤氏の上司として国見氏を追加するなら、次のようになります。
--1. 親の新規追加
INSERT INTO OrgChart
VALUES ('国見', (SELECT path FROM OrgChart WHERE emp = '上田') || '国見' || '/');
--2-1. 大神氏の部分木のパス更新
UPDATE OrgChart
SET path = REPLACE(path, '/' || '大神' || '/', '/' || '国見' || '/' || '大神' || '/')
WHERE path LIKE '%/' || '大神' || '/%';
--2-2. 加藤氏の部分木のパス更新
UPDATE OrgChart
SET path = REPLACE(path, '/' || '加藤' || '/', '/' || '国見' || '/' || '加藤' || '/')
WHERE path LIKE '%/' || '加藤' || '/%';
emp path
------ --------------------------
足立 /足立/
猪狩 /足立/猪狩/
上田 /足立/上田/
江崎 /足立/上田/江崎/
木島 /足立/上田/江崎/木島/
国見 /足立/上田/国見/ --親として追加
大神 /足立/上田/国見/大神/
加藤 /足立/上田/国見/加藤/
ループが必要になる、と言ったのは、第二段階の UPDATE 文を直下の子供の数だけ実行する必要があるためです。今回は二人なので、列挙しても大したことはありませんが、一般的にはプロシージャ内のループで処理するのが良いでしょう。
図3-4. 親を追加する
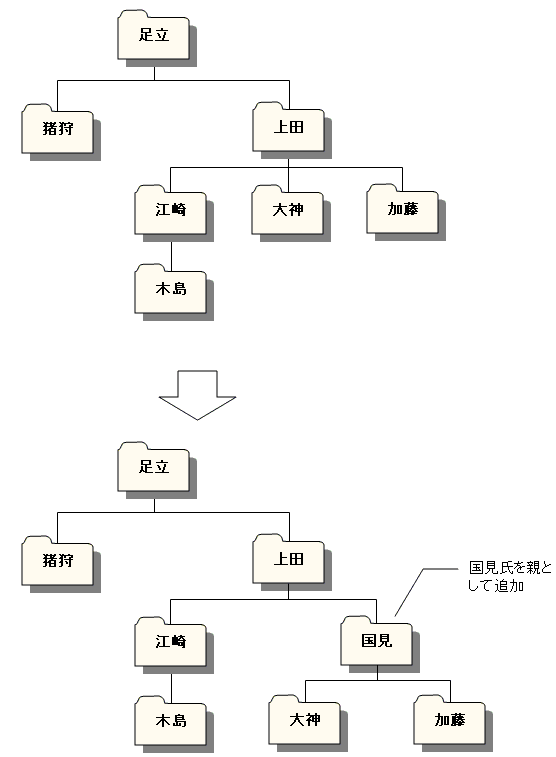
この方法ならば、現行のルートより上にノードを追加することもできます。その場合は、最初の INSERT で親パスを求めるスカラ・サブクエリは不要になります。SQL をわざわざ変えるのが面倒なら、テーブルに存在しないキーをパラメータに渡して、返ってきた NULL を空文字に変換するようなロジックにしておくのも、拡張的でよいかもしれません。
入れ子集合モデルでは、ノードをくるっと入れ替えるという器用な芸当も一つの SQL で可能でした。ほとんど同じ考え方で、経路列挙モデルでもいけます。単一ノードの入れ替えなら単純にパスを相互置換するだけですし、ごそっと部分木を入れ替えるのも次の SQL で可能です。ただし、パスが主キーの場合と番号の場合で SQL が異なります。
パスが番号の場合は簡単です。入れ替えたいノードのパスを :path_1、:path_2 というパラメータで渡してやります。
--部分木の入れ替え
UPDATE OrgChart
SET path = CASE WHEN path LIKE :path_1 || '%'
THEN REPLACE(path, :path_1, :path_2)
WHEN path LIKE :path_2 || '%'
THEN REPLACE(path, :path_2, :path_1)
ELSE path END
WHERE path LIKE :path_1 || '%'
OR path LIKE :path_2 || '%';
考え方としては、入れ替えたいノードをパスに含むようなノード全てについて、上層のパスを全部「:path_1 なら :path_2 へ、:path_2 なら :path_1」へ、チェンジしてやるわけです。例えば、猪狩氏と江崎氏の入れ替えなら次のようになります。
UPDATE OrgChart
SET path = CASE WHEN path LIKE '.1.1.' || '%'
THEN REPLACE(path, '.1.1.', '.1.2.1.')
WHEN path LIKE '.1.2.1.' || '%'
THEN REPLACE(path, '.1.2.1.', '.1.1.')
ELSE path END
WHERE path LIKE '.1.1.' || '%'
OR path LIKE '.1.2.1.' || '%';
emp path
------ --------------------------
足立 .1.
江崎 .1.1.
木島 .1.1.1.
上田 .1.2.
猪狩 .1.2.1.
大神 .1.2.2.
加藤 .1.2.3.
では、今度はパスが主キーである場合を考えましょう。これも基本的な考え方は番号の場合と同じままいけます。emp 列は当然入れ替えるとして、path 列についても、入れ替え対象の二人が現れている行すべてについて入れ替えます。入れ替え対象の emp を、:emp_1、:emp_2 として渡してやります。
UPDATE OrgChart
SET emp = CASE WHEN emp = :emp_1
THEN :emp_2
WHEN emp = :emp_2
THEN :emp_1
ELSE emp END,
path = CASE WHEN path LIKE '%' || :emp_1 || '%'
THEN REPLACE(path, :emp_1, :emp_2)
WHEN path LIKE '%' || :emp_2 || '%'
THEN REPLACE(path, :emp_2, :emp_1)
ELSE path END
WHERE path LIKE '%' || :emp_1 || '%'
OR path LIKE '%' || :emp_2 || '%';
例えば、猪狩氏と江崎氏を入れ替えるならこうなります。
UPDATE OrgChart
SET emp = CASE WHEN emp = '猪狩'
THEN '江崎'
WHEN emp = '江崎'
THEN '猪狩'
ELSE emp END,
path = CASE WHEN path LIKE '%' || '猪狩' || '%'
THEN REPLACE(path, '猪狩', '江崎')
WHEN path LIKE '%' || '江崎' || '%'
THEN REPLACE(path, '江崎', '猪狩')
ELSE path END
WHERE path LIKE '%' || '猪狩' || '%'
OR path LIKE '%' || '江崎' || '%';
emp path
---- ---------------------
足立 /足立/
江崎 /足立/江崎/
上田 /足立/上田/
猪狩 /足立/上田/猪狩/
木島 /足立/上田/猪狩/木島/
大神 /足立/上田/大神/
加藤 /足立/上田/加藤/
このクエリは、主キーを入れ替えているので、PostgreSQL や MySQL では一時的な主キー重複によってエラーが生じます。Oracle や DB2 など商用 DB では正しく動作します。
うーん、そうですねえ。一度入れ子集合モデルへ変換して、そこから経路列挙モデルに変換する、という二段階を踏むのはどうでしょう。
ちょいと面倒ですけど、確実な方法です。こんな変換しょっちゅうやるものじゃないし、どうでっしゃろ。え? 手を抜くな? 一発でやれるクエリを教えろ? しょうがないなあ・・・よっしゃ、まかしとき。次の SQL なら、木の高さを事前に調べておけば一発です。
INSERT INTO Orgchart_PE
SELECT T1.node,
'/' || COALESCE(T4.node || '/' , '')
|| COALESCE(T3.node || '/' , '')
|| COALESCE(T2.node || '/' , '')
|| T1.node || '/' AS path
FROM Tree T1
LEFT OUTER JOIN Tree T2
ON T1.parent = T2.node
LEFT OUTER JOIN Tree T3
ON T2.parent = T3.node
LEFT OUTER JOIN Tree T4
ON T3.parent = T4.node;
node path
----- ----------------------
足立 /足立/
猪狩 /足立/猪狩/
上田 /足立/上田/
江崎 /足立/上田/江崎/
大神 /足立/上田/大神/
加藤 /足立/上田/加藤/
木島 /足立/上田/江崎/木島/
結合条件の parent を辿って一つ一つ階層を上に昇っていく様子がお分かりいただけるでしょうか。いわばポインタ・チェインを SQL で辿っているわけです(お世辞にも SQL らしい SQL ではありません)。COALESCE は、もう上に親がいなかった場合、文字列結合に NULL が紛れ込んでパス全体が NULL になってしまうのを防ぐために入れています(そのため、Oracle のように空文字と NULL を混同している DB では、このコードは正しい結果を返しません。PostgreSQL では正しく動きます)。
なお、見て分かるように、隣接リストモデルから変換できるのはパスに主キーを使うケースだけです。番号を順序良く割り振るのは、かなりしんどいでしょう。
経路列挙モデルから隣接リストモデルの形式へ変換する方法は、入れ子集合モデルのときとほとんど同じです。
INSERT INTO OrgChart_AL
SELECT Worker.emp AS emp, Boss.emp AS boss
FROM OrgChart Worker
LEFT OUTER JOIN OrgChart Boss
ON Worker.path > Boss.path
AND Boss.path = (SELECT MAX(path)
FROM OrgChart
WHERE Worker.path LIKE path || '_%');
emp boss
------------
足立
猪狩 足立
上田 足立
江崎 上田
大神 上田
加藤 上田
木島 江崎
自分のパスを含むような親たちのうち、最大のパスが直近の親だ、という条件を記述しています。これは、パスが主キーでも番号でも大丈夫です。
またまた手抜き路線。一度入れ子集合モデルを間にかまします。そこから経路列挙モデルへの変換は、木の高さを調べておけば楽勝です。以下を参照。
とまあ、「XML → 入れ子集合モデル → 経路列挙モデル」というお手軽なのが一つ。面倒ですけど、そんな頻繁にやる作業でもないでしょうから、これでもいいと私は思いますが、XML からダイレクトに経路列挙モデルへ変換する方法があれば、それにこしたことはありません。どうでしょう、何かよいアイデアはないでしょうか。皆さんも考えてみてください。
これまでは、一つの木についてその内部構造を調べたり、操作したりしてきました。しかし例えば、テーブルの環境を移動したり、バックアップをとったりしたときに、二つの木が同型であるか、全く同じノードを含んでいるのか、ということを調べる必要が生じることもあります。そこでここでは、二つの木を比較することを考えましょう。この比較をするときに重要な役割を果たすのが、集合演算子が持つ冪等性という性質を利用したテーブルの同一性チェックの方法です(詳細は「SQLで集合演算」を参照)。
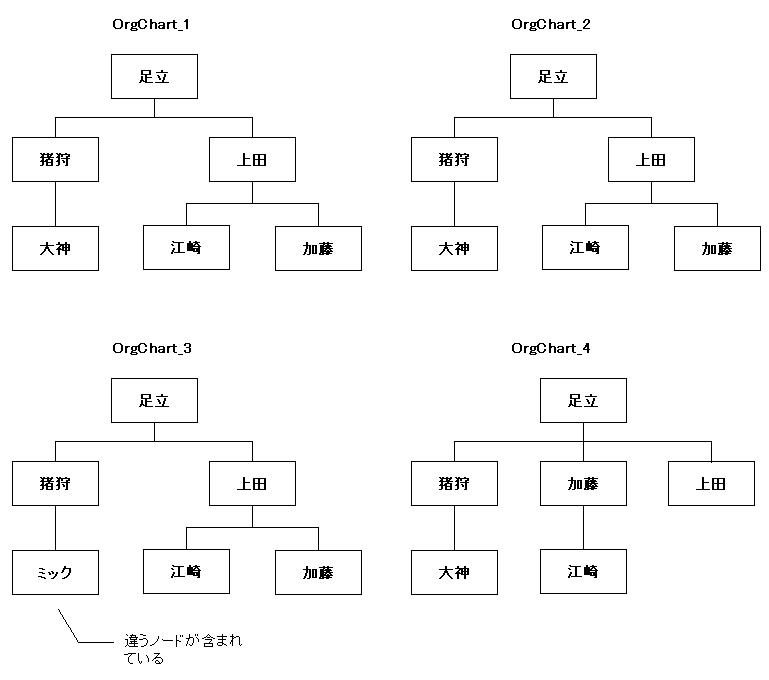
サンプル・データとして、次の四つのテーブルを用意しましょう。
図4. 木同士の比較
CREATE TABLE OrgChart_1
(emp VARCHAR(32) PRIMARY KEY
CHECK (REPLACE(emp, '/', '') = emp),
path VARCHAR(256) NOT NULL,
UNIQUE (path));
DELETE FROM OrgChart_1;
INSERT INTO OrgChart_1 VALUES ('足立', '/足立/');
INSERT INTO OrgChart_1 VALUES ('猪狩', '/足立/猪狩/');
INSERT INTO OrgChart_1 VALUES ('上田', '/足立/上田/');
INSERT INTO OrgChart_1 VALUES ('江崎', '/足立/上田/江崎/');
INSERT INTO OrgChart_1 VALUES ('大神', '/足立/上田/大神/' );
INSERT INTO OrgChart_1 VALUES ('加藤', '/足立/上田/加藤/' );
CREATE TABLE OrgChart_2
(emp VARCHAR(32) PRIMARY KEY
CHECK (REPLACE(emp, '/', '') = emp),
path VARCHAR(256) NOT NULL,
UNIQUE (path));
DELETE FROM OrgChart_2;
INSERT INTO OrgChart_2 VALUES ('足立', '/足立/');
INSERT INTO OrgChart_2 VALUES ('猪狩', '/足立/猪狩/');
INSERT INTO OrgChart_2 VALUES ('上田', '/足立/上田/');
INSERT INTO OrgChart_2 VALUES ('江崎', '/足立/上田/江崎/');
INSERT INTO OrgChart_2 VALUES ('大神', '/足立/上田/大神/' );
INSERT INTO OrgChart_2 VALUES ('加藤', '/足立/上田/加藤/' );
CREATE TABLE OrgChart_3
(emp VARCHAR(32) PRIMARY KEY
CHECK (REPLACE(emp, '/', '') = emp),
path VARCHAR(256) NOT NULL,
UNIQUE (path));
DELETE FROM OrgChart_3;
INSERT INTO OrgChart_3 VALUES ('足立', '/足立/');
INSERT INTO OrgChart_3 VALUES ('猪狩', '/足立/猪狩/');
INSERT INTO OrgChart_3 VALUES ('上田', '/足立/上田/');
INSERT INTO OrgChart_3 VALUES ('江崎', '/足立/上田/江崎/');
INSERT INTO OrgChart_3 VALUES ('ミック', '/足立/上田/ミック/' ); --違うノードが含まれている
INSERT INTO OrgChart_3 VALUES ('加藤', '/足立/上田/加藤/' );
--ノードは同じだが、構造が異なる
CREATE TABLE OrgChart_4
(emp VARCHAR(32) PRIMARY KEY
CHECK (REPLACE(emp, '/', '') = emp),
path VARCHAR(256) NOT NULL,
UNIQUE (path));
DELETE FROM OrgChart_4;
INSERT INTO OrgChart_4 VALUES ('足立', '/足立/');
INSERT INTO OrgChart_4 VALUES ('猪狩', '/足立/猪狩/');
INSERT INTO OrgChart_4 VALUES ('大神', '/足立/猪狩/大神/');
INSERT INTO OrgChart_4 VALUES ('加藤', '/足立/加藤/');
INSERT INTO OrgChart_4 VALUES ('江崎', '/足立/加藤/江崎/');
INSERT INTO OrgChart_4 VALUES ('上田', '/足立/上田/');
OrgChart_1 と OrgChart_2 は、構造もノードも全く同じ、すなわちテーブル名が違うだけで集合としては完全に同一であると言うことができます。OrgChart_3 は、構造は 1, 2 と同じですが、木を構成しているノードが異なります。OrgChart_4 は反対に、ノードは全く同じですが、構造が異なります。
構造も同型、使われているノードもピッタリ同じ、ということは、平たく言えばテーブルとして相等だということです。従って、単純にテーブルの相等性チェックのクエリが使えます。代表的なものは、次の二つです。
--木の相等性チェック:その1
SELECT CASE WHEN COUNT(*) = (SELECT COUNT(*) FROM OrgChart_1 )
AND COUNT(*) = (SELECT COUNT(*) FROM OrgChart_2 )
THEN '等しい'
ELSE '異なる' END AS result
FROM ( SELECT * FROM OrgChart_1
UNION
SELECT * FROM OrgChart_2 ) TMP;
--木の相等性チェック:その2
SELECT DISTINCT CASE WHEN COUNT(*) = 0
THEN '等しい'
ELSE '異なる' END AS result
FROM ((SELECT * FROM OrgChart_1
UNION
SELECT * FROM OrgChart_2)
EXCEPT
(SELECT * FROM OrgChart_1
INTERSECT
SELECT * FROM OrgChart_2)) TMP;
どちらのクエリも、1番と2番の木を比較したときのみ「等しい」を返し、残る組み合わせについては全て「異なる」を返します。パフォーマンスについては、どちらも似たりよったりだと思いますが、最初のクエリは UNION しか使わないので、INTERSECT や EXCEPT をサポートしていない MySQL や MS-Access でも使えるという利点があります。
このクエリは、パスに主キーを使った場合、番号を使った場合の双方に通用します。
今度は、構造としての同型性は無視して、とにかく木に含まれているノードが同一なのかどうかを調べることを考えます。これもさっきのクエリを少し改変するだけで簡単に実現できます。このモデルでは、構造はパス列によって表現されていますから、この列を除外して比較すれば OK です。
--ノードの相等性チェック:その1
SELECT CASE WHEN COUNT(*) = (SELECT COUNT(*) FROM OrgChart_1 )
AND COUNT(*) = (SELECT COUNT(*) FROM OrgChart_3 )
THEN '等しい'
ELSE '異なる' END AS result
FROM ( SELECT emp FROM OrgChart_1
UNION
SELECT emp FROM OrgChart_3 ) TMP;
--ノードの相等性チェック:その2
SELECT DISTINCT CASE WHEN COUNT(*) = 0
THEN '等しい'
ELSE '異なる' END AS result
FROM ((SELECT emp FROM OrgChart_1
UNION
SELECT emp FROM OrgChart_3)
EXCEPT
(SELECT emp FROM OrgChart_1
INTERSECT
SELECT emp FROM OrgChart_3)) TMP;
今度は、1、2、4番の木は、互いにどれを比較しても「等しい」という判定になります。4番は構造は異なるものの、ノードは1、2番と同一だからです。一方、3番は他のどの木比較しても「異なる」とされます。「ミック」という邪魔者を含んでいるからです。もちろん、そもそも木の間でノードの数が不一致な場合でも正しく判定できます。パスを使わないので、このクエリも当然、パスが主キーでも番号でも使えます。
ではラストの問題です。今度は使われているノードは一切無視して、木の構造のみに着目します。とすれば、何を比較すればよいかは・・・もうお分かりですね。そう、パス列が完全一致するかどうかを調べればよいのです。ただしこのケースでは、主キーに番号を使っている場合でしか動作しません。パスに主キーを使っていると、構造とノードの情報が一つの列に分離せずに収められている状態であるため、こういう両者を分離したい場合には不便です。
--構造の同型性チェック:その1
SELECT CASE WHEN COUNT(*) = (SELECT COUNT(*) FROM OrgChart_1 )
AND COUNT(*) = (SELECT COUNT(*) FROM OrgChart_4 )
THEN '等しい'
ELSE '異なる' END AS result
FROM ( SELECT path FROM OrgChart_1
UNION
SELECT path FROM OrgChart_4 ) TMP;
--構造の同型性チェック:その2
SELECT DISTINCT CASE WHEN COUNT(*) = 0
THEN '等しい'
ELSE '異なる' END AS result
FROM ((SELECT path FROM OrgChart_1
UNION
SELECT path FROM OrgChart_4)
EXCEPT
(SELECT path FROM OrgChart_1
INTERSECT
SELECT path FROM OrgChart_4)) TMP;
木の構造としては、1〜3の木は同型ですから、これらのどれを比較しても「等しい」となります。4番は、他のいずれとも異なる形をしているので、「異なる」と見なされます。
ここでは、他の言語、または様々なデータベースの実装で入れ子集合モデルを扱うためのライブラリやツール類、それに各種情報ソースを紹介します。
準備中。情報求む。
この本の主眼は入れ子集合モデルにありますが、経路列挙モデルも二番目ぐらいの重要性で扱われています。「3 Path Enumeration Models」を参照。
理論的な解説というよりは、パフォーマンス上の比較がメインですが、次の書籍で日本語で読むことができます。
セルコの解説は Web 上でも読むことができます。以下を参照
現在調査中。情報求む。
作成者:ミック
作成日:2007/10/07
最終更新日:2007/10/07

この作品は、クリエイティブ・コモンズ・ライセンスの下でライセンスされています。











